Analysis of Seismic Response of Bridge across Earthquake Fault with Different Input Modes of Seismic Action
-
摘要: 大地震在近断层场地产生强烈地震动的同时，还会由于断层错动直接导致基岩甚至上覆土层破裂，在断层两侧产生显著差异性永久位移，造成位于断层附近或跨越断层的工程结构破坏。因此，跨断层桥梁面对的地震作用是断层两侧桥墩处场地的不同地震动，包括存在永久性位移的地震动。本文以垂直跨越走滑断层的多跨简支梁桥为例，基于OpenSees有限元模拟平台建立了桥梁结构的三维计算模型，计算分析了不同地震作用输入模式下桥梁结构的地震反应及其差异。考虑的地震作用模式包括：（1）断层两侧场地的地震作用视为相同的无永久位移的地震动，即无永久位移的一致地震动作用模式；（2）断层主动盘一侧场地的地震作用具有永久位移地震动，被动盘一侧采用无永久位移地震动，即具有永久位移的非一致地震动作用模式；（3）在断层主动盘一侧场地以静力方式施加断层错动位移，而被动盘一侧场地固定不动，即断层错动位移静力作用模式。计算结果分析表明，不考虑永久位移的一致地震动作用模式的地震动输入会导致严重低估桥梁反应计算结果，这也说明地震动的断层两侧永久性位移差异会显著增大桥梁结构反应；而一致地震动作用叠加断层错动永久位移静力作用的结果与非一致地震动作用模式的结果非常接近。为此，在某种程度上说，跨断层桥梁结构地震反应可采用一致地震动作用叠加断层错动位移静力作用的桥梁结构反应来近似模拟。Abstract: A large earthquake can produce strong ground motion at the near-fault site, and at the same time, it may directly break up the bedrock and even the overlying soil layers due to fault rupture, which leads to significant differential permanent displacement on both sides of the fault, and results in severe damage of the structure located near or crossing fault. Therefore, the seismic action on the bridge across fault is different on both sides of the fault, including the ground motion with permanent displacement. A simply supported girder bridge vertically across strike-slip fault is taken as an example, and a three-dimensional fnite-element model is developed using the earthquake engineering simulation software framework OpenSees (Open System for Earthquake Engineering Simulation). The seismic response of the bridge structure under different modes of seismic action is analyzed. The modes of seismic action considered include: (1) Seismic action of sites on both sides of the fault is regarded as the same ground motion without permanent displacement, that is, a consistent ground motion mode of seismic action without permanent displacement; (2) Seismic action of sites is regarded as a ground motion with permanent displacement on the active side of the fault, and a ground motion without permanent displacement on the passive side of the fault, that is, a non-consistent ground motion mode of seismic action with permanent displacement; (3) Fault dislocation displacement is applied to the site on the active side of fault, while the site on the passive side is fixed, that is, a static force mode of seismic action with fault dislocation displacement. The analysis results show that a consistent ground motion mode of seismic action without permanent displacement leads to a significant underestimation of the bridge structure responses, which indicates that the difference of permanent displacements of ground motions on both sides of the fault significantly increases the bridge structure response; The result from the superposition of the consistent ground motion mode and static force mode of fault dislocation permanent displacement is very close to the result from the non-consistent ground motion mode. Therefore, to a certain extent, the seismic response of cross-fault bridge structures can be approximately simulated by combining a consistent ground motion mode and a static force mode of fault dislocation displacement.
-
引言
近断层地震动十分复杂，地震动特性受断层破裂类型、断层破裂过程及局部场地条件等因素影响，具有方向性、速度大脉冲和永久位移等一系列与远场地震动不同的特征（Somerville，2003；周正华等，2003；刘启方等，2006；李小军等，2012；袁一凡等，2012；惠迎新等，2017）。强震震害调查显示，近断层地震动除强度大导致工程结构破坏外，其丰富的长周期成分、速度大脉冲、大位移及永久位移等特性会加重对工程结构的破坏，造成桥梁上部结构过度移动、桥梁支座以及隔震消能系统失效等破坏，致使桥梁结构产生灾难性的、不可恢复的破坏（Byers等，2000；Ghasemi等，2000；Imbsen等，2000）。已有典型震例包括，1976年唐山大地震中滦河大桥的落梁破坏（王东升等，2005）；1995年日本阪神地震中高架桥倾倒破坏（Kitagawa等，2004）； 1999年我国台湾集集地震中乌溪桥、名竹桥、长庚桥、埤丰桥等多座桥梁由于断层错动引起的地面大变形和近地表破裂导致落梁、桥墩倾斜等损毁（Chang等，2000；Hsu等，2004；惠迎新等，2014）；2008年四川汶川大地震中高树大桥、小鱼洞大桥等桥梁因断层穿过而发生严重破坏甚至垮塌（杜修力等，2008；刘爱文等，2008；王东升等，2009）。
大地震中跨断层工程结构会因强烈地震动及断层错动引起的场地地表大变形和破裂的综合作用遭受到严重损害。因此，各国工程设计规范一般要求工程场地避让大型活动断层（EN 1998-5—2004《Eurocode 8：design of structures for earthquake resistance Part 5：foundation，retaining structures and geotechnical aspects》（CEN，2004）；GB 50011—2010《建筑抗震设计规范》（中华人民共和国住房和城乡建设部等，2010）；Caltrans，2012；JTG B02—2013《公路工程抗震规范》（中华人民共和国交通运输部，2014））。我国的JTG/T 2231-01—2020《公路桥梁抗震设计规范》（中华人民共和国交通运输部，2020）规定：A类桥梁宜避开主断裂，抗震设防烈度为Ⅷ度和Ⅸ度地区的桥墩边缘至主断裂带外缘的距离分别不宜小于300 m和500 m。但随着我国生命线工程建设的发展，公路和铁路工程的桥梁不可避免地需要邻近或者跨越大型活动断层，如跨越铺前湾的海南海文大桥位于1605年琼山7½级大地震的震中区，桥梁横跨这次地震的发震断层（铺前-清澜大型活动断层）。在地震活跃的美国加州，据估计超过5%的桥梁可能会跨越或位于断层破裂带附近；我国西部地区越来越多的桥梁建设也面临跨越活动断层的问题。美国加州交通局（Caltrans，2012）提出适应于跨越走滑断层普通桥梁的线性准静力简化分析方法作为AASHTO规范和Caltrans抗震设计标准的补充（Goel等，2008），并提出位于活动断层300英尺范围内的桥梁需依据项目特定的抗震设计标准（PSDC）进行断层破裂危险性分析和设计（Caltrans，2019）。在我国，JTG/T 2231-01—2020《公路桥梁抗震设计规范》也增加了相关规定，如当桥位无法避开活动断层且不能将全部墩台布置在断层的同一盘时宜进行专项研究，以提出针对性的跨越活动断层措施，降低断层地表破裂带来的地震破坏风险。
跨断层桥梁结构抗震问题越来越受到国内外学者关注，相应地开展了一些研究工作（李鸿晶等，2009；王东升等，2010；李建中等，2011；Mackie等，2012；Sengupta等，2016；Li等，2017；Wang等，2017）。Roussis等（2003）、Park等（2004）、Güney等（2010）等学者对1999年土耳其Duzce地震中严重破坏的跨断层Bolu高架桥进行了非线性有限元时程抗震性能分析，表明在速度大脉冲地震动及断层错动地表破裂共同作用下，支座和消能单元严重损坏，指出纵向和横向的抗剪挡块在防止桥跨倒塌中起着关键作用。Goel等（2009a，2009b，2014）对美国加州跨断层的典型标准钢筋混凝土桥梁进行了一系列地震反应分析，提出了适应于跨走滑断层普通桥梁的反应谱法和线性/非线性准静力简化分析方法。惠迎新等（2015a，2015b，2015c）从地震动输入方法、桥梁地震反应特征、断层穿越位置与角度影响等方面对跨断层桥梁的抗震问题开展一系列研究，提出了包括结构形式、抗震措施等方面的抗震设计原则。杨怀宇等（2015）利用已有脉冲模型生成模拟断层效应的地面运动，采用非一致激励时程分析方法研究了跨断层桥梁结构地震反应，结果表明紧邻断层的桥墩墩底弯矩以及墩顶处横向支座位移相较其他位置桥墩大很多，如果不考虑断层位错的影响，将会低估桥梁结构的响应需求。Yang等（2018）系统回顾了跨断层桥梁相关的震害调查、试验、理论分析和数值研究结果，对跨断层桥梁抗震设计规范做出总结。上述研究工作表明，跨断层桥梁的地震反应受到包括地震震级、断层穿越角度等各种参数的影响。针对地震断层错动引起的断层两侧永久性地面大变形差异对桥梁结构抗震性能影响的研究仍较少。
跨断层桥梁结构抗震分析涉及的一个主要问题就是地震作用，即跨断层工程场地地震动的确定。一般根据工程场地地震环境、发震断层信息和抗震设计需要，在强震动记录库中选择条件相近的近断层观测数据，通过适当调整观测记录的幅值、持时等地震动参数，作为地震动输入（Sehhati等，2011；石岩等，2014；陈令坤等，2016）。在难以得到合适的近断层强地震动记录情况下，通过实际地震记录叠加等效数学脉冲模型的方法人工合成地震动成为发展趋势（Makris等，2000；Mavroeidis等，2003；He等，2008；江辉等，2011；Yan等，2015；管仲国等，2016）。李帅等（2017）提出近断层脉冲型地震动合成的“分解-叠加”方法，即通过地震动分解法得到近断层高频地震动，再叠加等效脉冲模型得到合成近断层地震动。
本文以跨越走滑断层的多跨简支梁桥为例开展研究，探讨所跨越断层发生地震引起强烈地震动和工程场地地面错动永久位移的情况下跨断层桥梁结构反应及其特征，特别是探讨采用不同地震作用输入模式时桥梁结构反应计算结果的差异。
1. 桥梁结构地震反应计算模型和分析方法
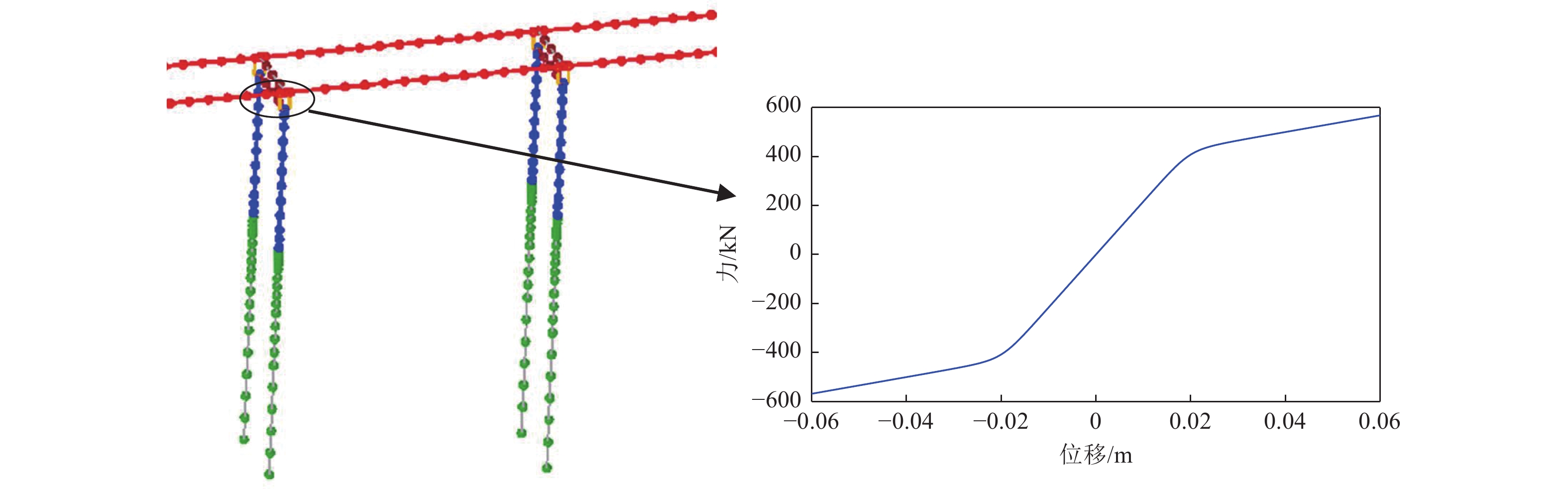
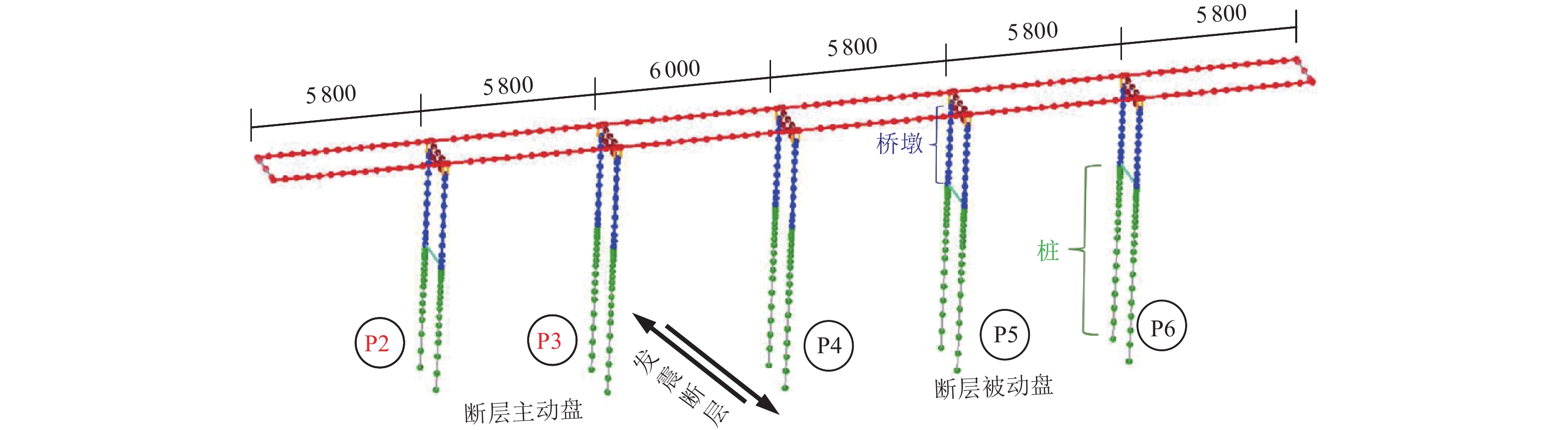
以海文大桥（原名“铺前大桥”）工程为背景建立场地和桥梁计算分析模型，本文选取整体桥梁中的断层两侧6跨进行具体计算分析，如图1所示。设定桥梁在第3跨与断层垂直相交，即P2、P3号桥墩与P4、P5、P6桥墩分别位于断层两侧。桥梁跨度组合设计为2×58 m+60 m+3×58 m，桥面宽32 m，梁高2.8 m。所有桥墩设计为双柱式钢筋混凝土空心墩，壁厚均为0.55 m，而墩高不同，分别为33.1 、31.6 、30.1 、28.7 、27.2 m。为提高桥梁结构的抗震性能，桥墩与主梁之间采取减隔震支座、断层错位调节装置等针对性的桥梁结构抗震设计。
选用由美国太平洋地震研究中心（PEER）开发的大型开源有限元平台OpenSees 构建桥梁结构的有限元计算模型（图1），其中断层错动主动盘一侧为2跨（包括P2、P3号桥墩）、断层错动被动盘一侧为3跨（包括P4、P5、P6号桥墩）。计算模型中，采用线弹性梁柱单元模拟大桥的桥墩和钢箱梁；考虑到桥墩和简支钢箱梁板之间有水平向相对位移，并且支座处在受力时纵向弯矩为0，采用双节点连接单元模拟主梁和桥墩之间的支座，单元材料采用单轴各向同性强化的Guiffre-Menegotto-Pinto钢材本构（Steel02），其屈前刚度、屈后刚度和屈服强度分别为21.6 kN∙mm−1，3.4 kN∙mm−1和432.0 kN，支座的力-位移关系如图2所示。桥梁两侧土-桥台相互作用分别通过2组线性弹簧单元模拟，结构阻尼采用5%的瑞利阻尼模型模拟。地震响应动力方程求解选用OpenSees中提供的Newmark平均加速度法。P2至P6号桥墩下方均为4×4的钻孔群桩，桩长44.0～63.0 m。为减小运算量，在有限元模型中将群桩简化为等效单桩。桩-土相互作用通过沿桩长每1～4 m设置1个p-y零长度弹簧（Zero Length Element）模拟，实现不同深度对应不同的应力应变关系。弹簧间距由上自下从1 m不断增大至4 m。土弹簧杆的单元刚度参照Elgamal等（2014）提供的p-y曲线。
2. 地震作用输入模式
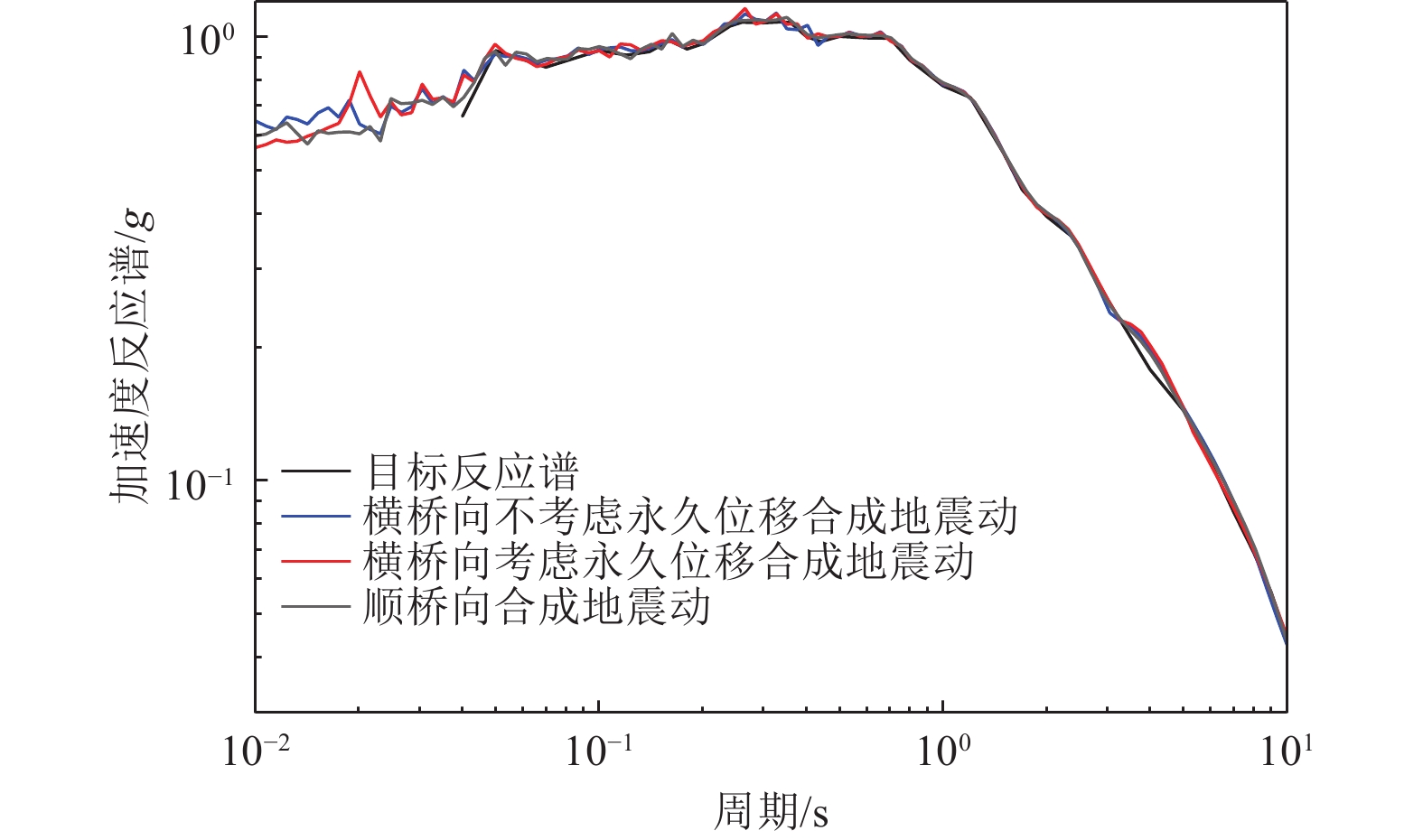
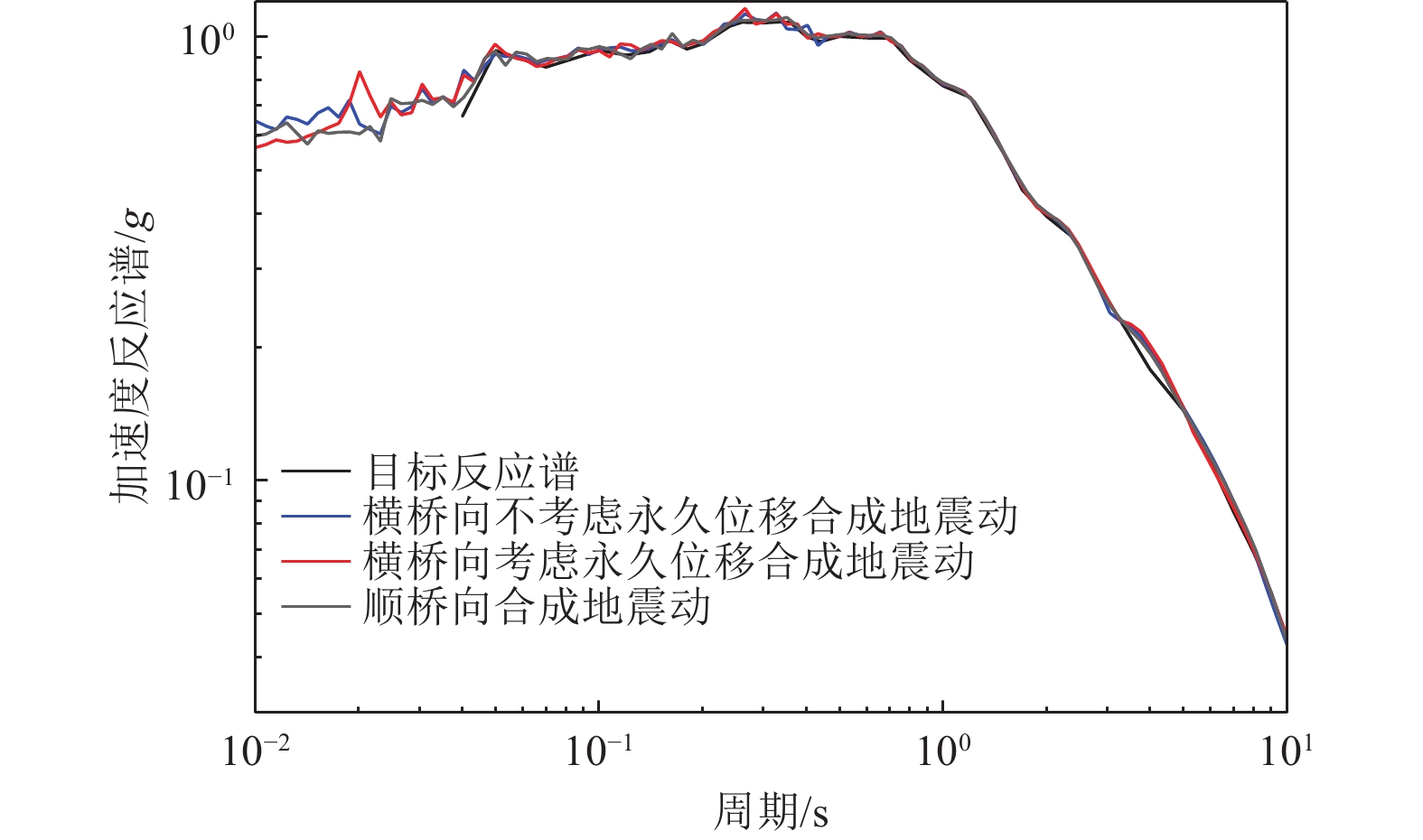
假设桥梁垂直跨越走滑型活动断层，该断层发震产生地震动和断层地表破裂。参考相关工程场地的地震安全性评价结果，场地基岩地震动参数为：断层左右两侧的横桥向水平永久位移（位错量）分别为0.81 m和0 m，而顺桥向水平永久位移量均为0 m；断层两侧的横桥向和顺桥向水平地震动峰值加速度和加速度反应谱均取相同值，峰值加速度为0.60 g，加速度反应谱如图3所示。本文计算中未考虑竖向地震动，假设为水平双向基岩地震动输入。
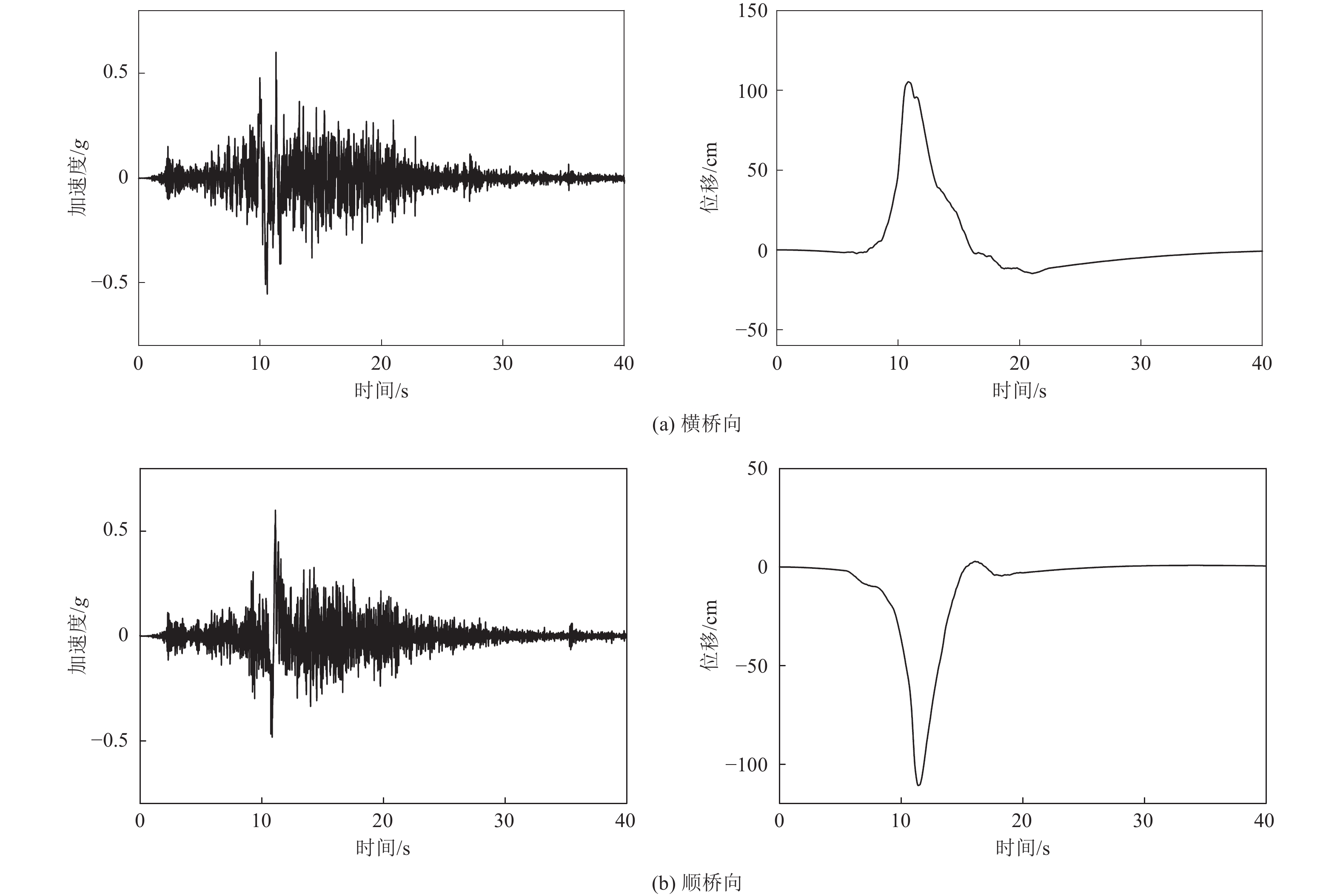
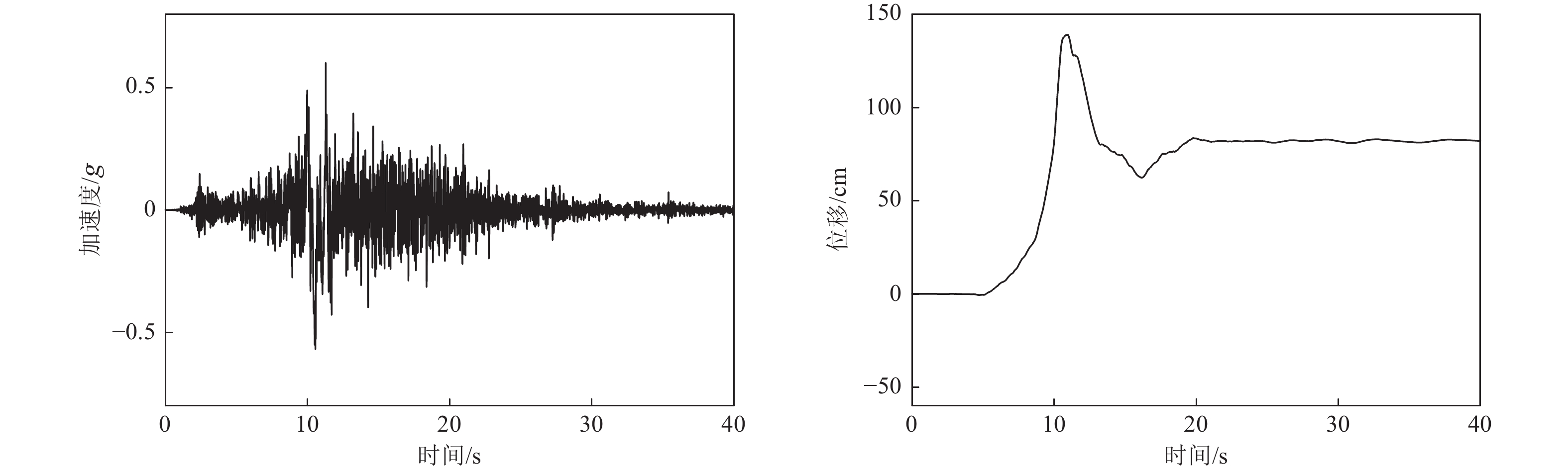
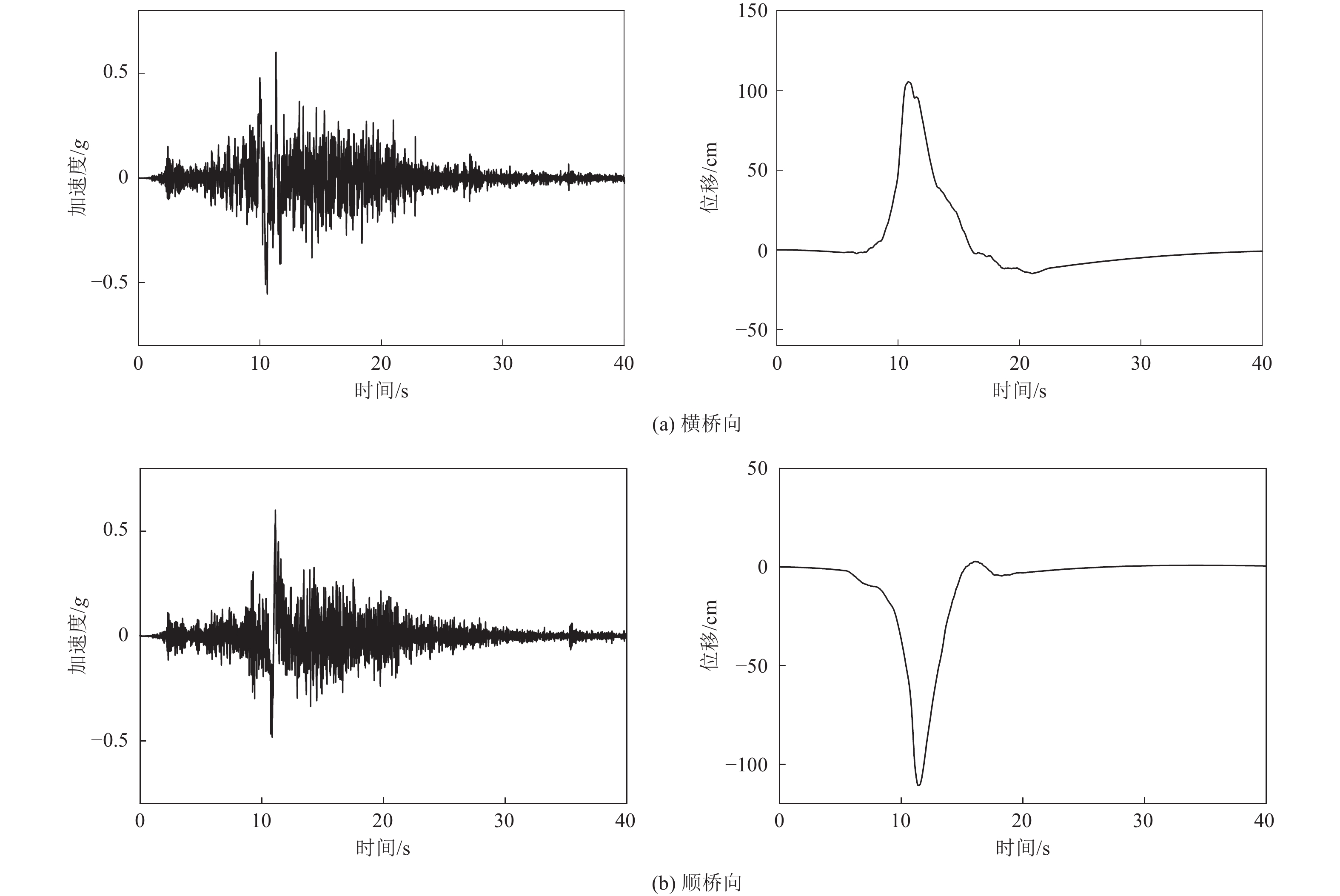
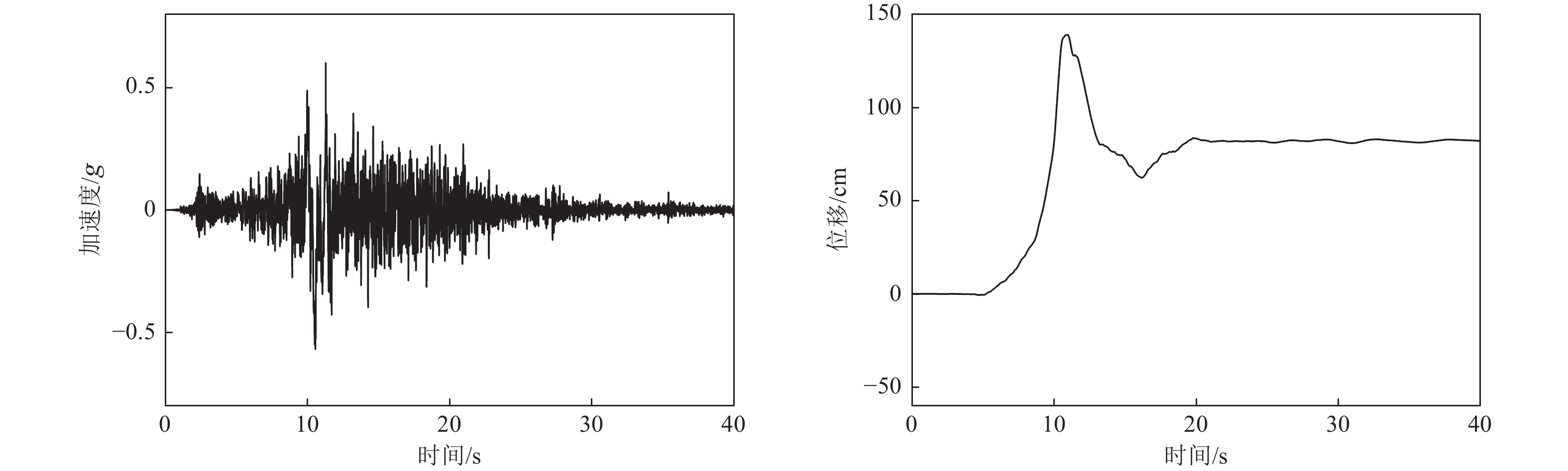
图 3 场地基岩水平向地震加速度反应谱Figure 3. Horizontal seismic acceleration response spectrum of rock site基于以上确定的场地基岩地震动峰值加速度、永久位移及加速度反应谱参数，人工合成相应的地震动时程。以1992年Landers地震（M7.3）的加速度记录为初始地震动时程，该记录台站的断层距（Joyner-Boore Distance）为2.19 km，地震动时程信息如表1所示。通过叠加单脉冲函数拟合满足目标加速度反应谱和峰值加速度的具有速度脉冲特性的地震动时程，包括含有与不含永久性位移的地震动加速度时程，地震动时程时间步长为0.005 s，持时为40.96 s，如图4、图5所示。人工合成的地震动峰值加速度、速度和位移数据如表2所示。
表 1 原始地震动时程信息Table 1. Original ground motion parameters方向 PGA /g PGV/（cm·s−1） PGD/cm 横桥向 0.73 133.33 113.87 顺桥向 0.79 28.09 25.52 
图 4 不考虑永久位移的人工合成地震动时程Figure 4. Synthetic ground motion time histories without considering permanent displacement
图 5 横桥向考虑永久位移的人工合成地震动时程Figure 5. Synthetic ground motion time history considering permanent displacement in the transverse direction表 2 合成的地震动时程信息Table 2. Synthetic ground motion parameters类别 PGA /g PGV /（cm·s−1） PGD /cm 横桥向不考虑永久位移 0.60 111.97 105.39 横桥向考虑永久位移 0.60 117.79 138.88 顺桥向不考虑永久位移 0.60 118.89 110.84 开展跨断层桥梁地震反应分析计算时，采用以下3种地震作用输入模式：
模式1：不考虑断层错动永久位移，断层左右两侧场地基岩采用一致性地震动输入，即无永久位移的一致地震动作用模式。
模式2：断层左侧的横桥向地震动考虑永久位移，断层左右两侧场地基岩采用非一致性地震动输入，即具有永久位移差的非一致地震动作用模式。
模式3：在断层左侧场地基岩以静力方式施加永久位移，而断层右侧场地基岩设定静止不动，即断层错动位移静力作用模式。这种模式中，位移施加方式为在一段时间内将位移逐级增加至要求的永久位移值，加载至永久位移值的时间与模式2中位移时程进入永久位移阶段的时间一致，本文算例中的具体时间约20 s（图5），后续保持加载位移值不变。
本文考虑桥梁场地为基岩半空间上覆成层土层场地，且断层两侧的覆盖土层相同，桥墩桩基位于覆盖土层中。首先基于桥梁工程场地地震安全性评价工作提供的场地勘测资料建立一维成层土层计算模型，并利用等效线性化频域土层反应计算方法（李小军，1992；李小军等，2001），分别以考虑与不考虑永久位移的基岩地震动时程作为基岩半空间入射波，进行场地土层地震反应计算分析，给出覆盖土层不同深度位置的场地地震动加速度时程；而后以土层中不同深度位置的地震动作为桥梁有限元模型中桩基相应深度处p-y弹簧场地端的输入运动，进行桥梁地震反应计算分析。
3. 桥梁地震反应计算及不同地震作用反应特征与差异分析
针对建立的桥梁结构有限元模型，分别采用上文确定的3种地震作用输入模式，计算桥梁墩顶相对位移、桥墩支座变形、桥墩墩底剪力、桥墩墩底弯矩和桥墩墩底扭矩等反应量。桥梁结构地震反应分析时，分别将地震作用输入模式1和模式2的计算记为工况1和工况2，将地震作用输入模式3和模式1的桥梁反应叠加计算记为工况3。
3.1 桥墩墩顶位移的响应
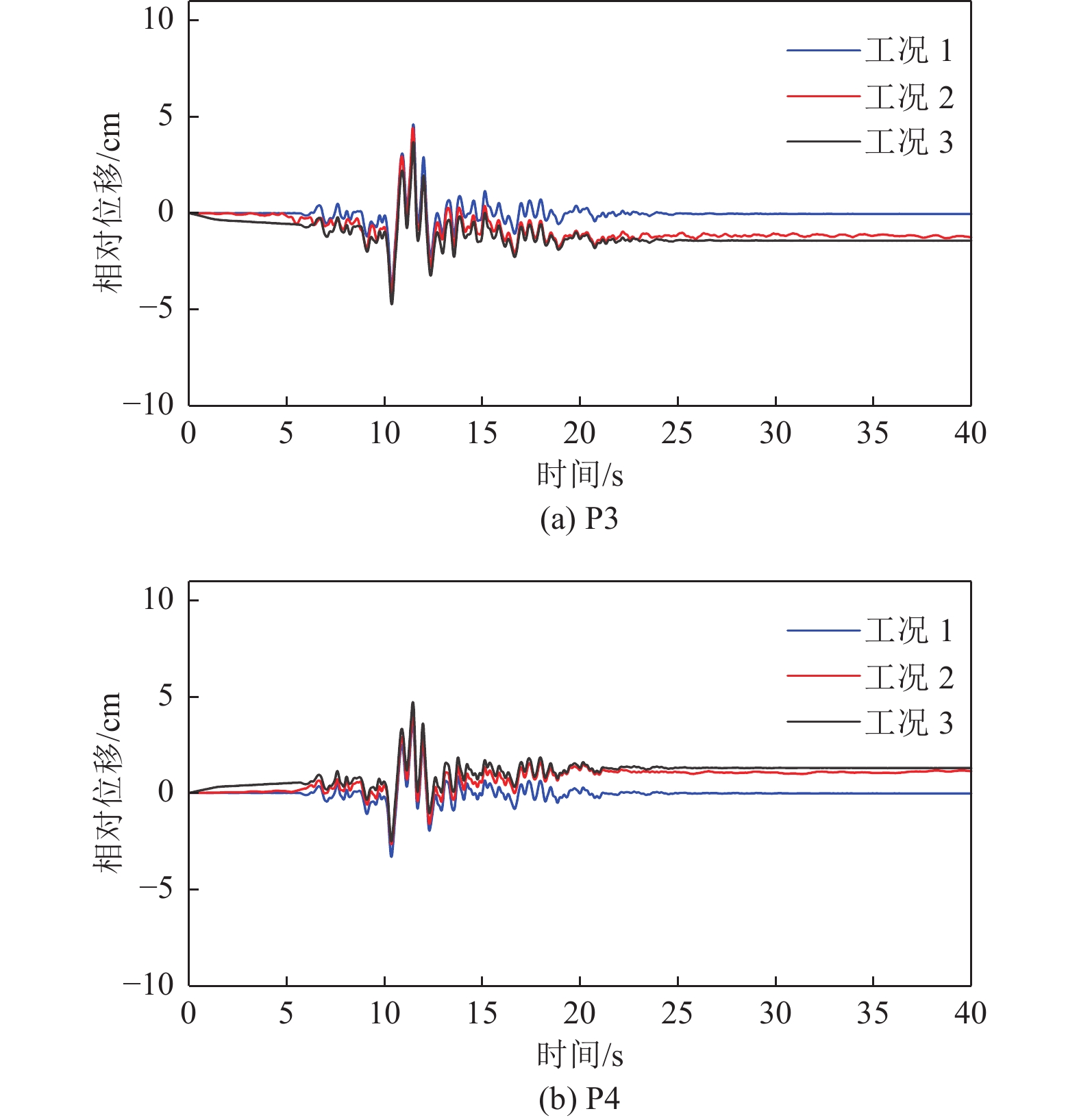
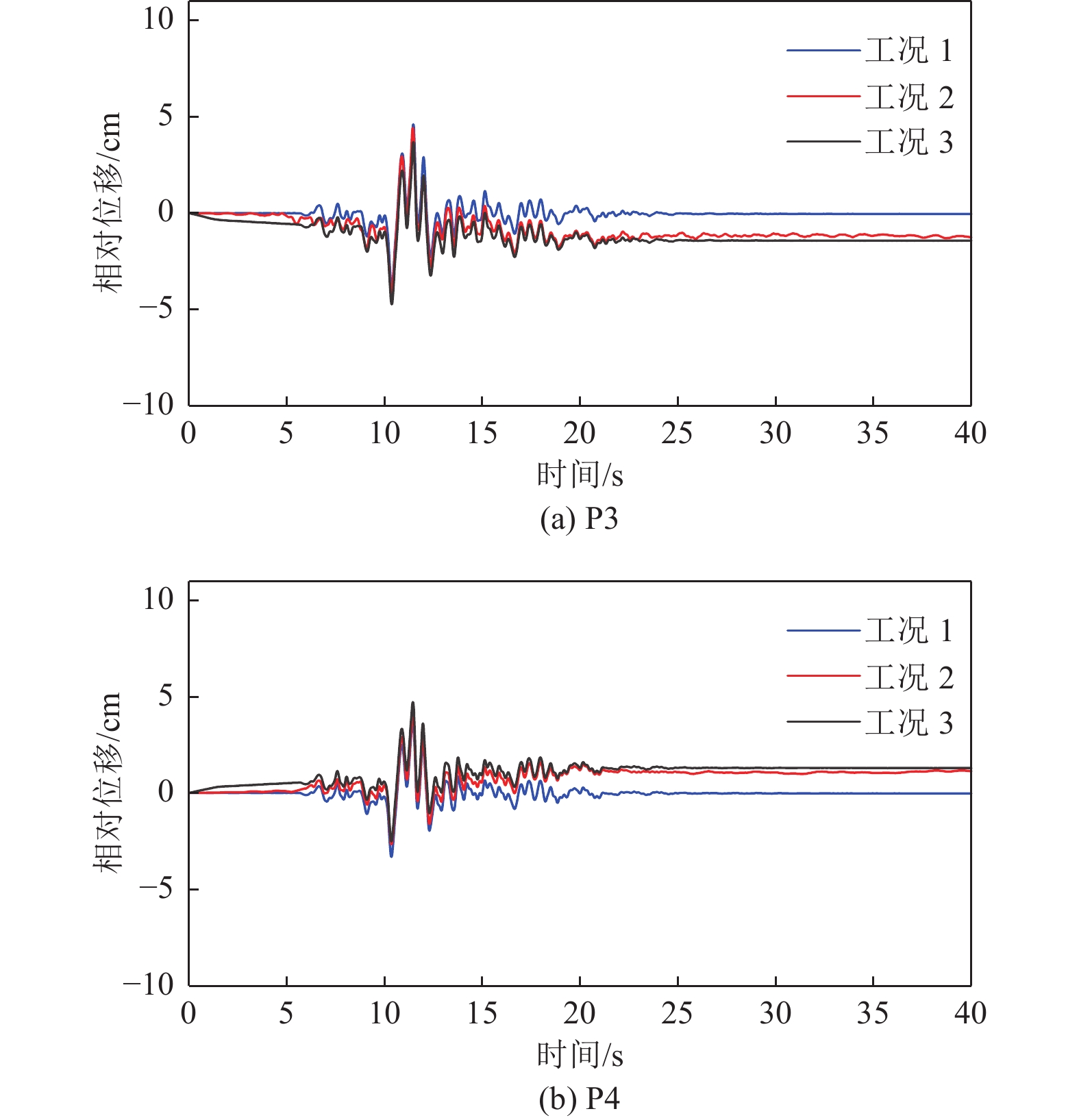
3种工况下横桥向墩顶相对位移时程如图6，相对位移最大值和残余值如表3所示。从计算结果可以看出，非一致地震动作用模式（工况2）和一致地震动作用模式（工况1）的地震动输入导致桥墩顶相对位移反应计算结果产生较大的差异。这说明地震动永久性位移及断层两侧地震动差异会使桥梁墩顶的相对位移显著增加；同时，非一致地震动作用模式（工况2）与一致地震动作用叠加断层错动位移静力作用（工况3）结果的比较，表明两者具有较好的一致性，工况3也能较好地反映断层两侧地震动（包括永久性位移）差异对桥梁反应墩顶相对位移的影响，特别是对断层两侧离断层最近的桥墩P3和P4，其最大值和残余值基本相同。
图 6 横桥向P3和P4墩顶相对位移时程Figure 6. Relative displacement time histories on the top of pier P3 and P4 in the transverse direction表 3 横桥向P3和P4墩顶相对位移最大值和残余值Table 3. Maximum and residual relative displacement of the pier top at P3 and P4 in the transverse direction工况 最大值/cm
（残余值/cm）P2 P3 P4 P5 P6 1 9.0580
（−0.1654）4.6155
（−0.0405）3.8598
（−0.0254）6.4269
（−0.1254）5.5834
（−0.1095）2 9.8470
（0.2830）4.4210
（−1.2270）4.1927
（1.1377）6.3951
（−0.0789）5.5772
（−0.0757）3 9.2286
（0.1558）4.7349
（−1.4285）4.7175
（1.2923）6.4440
（−0.1007）5.5611
（−0.1431）3.2 桥墩支座变形
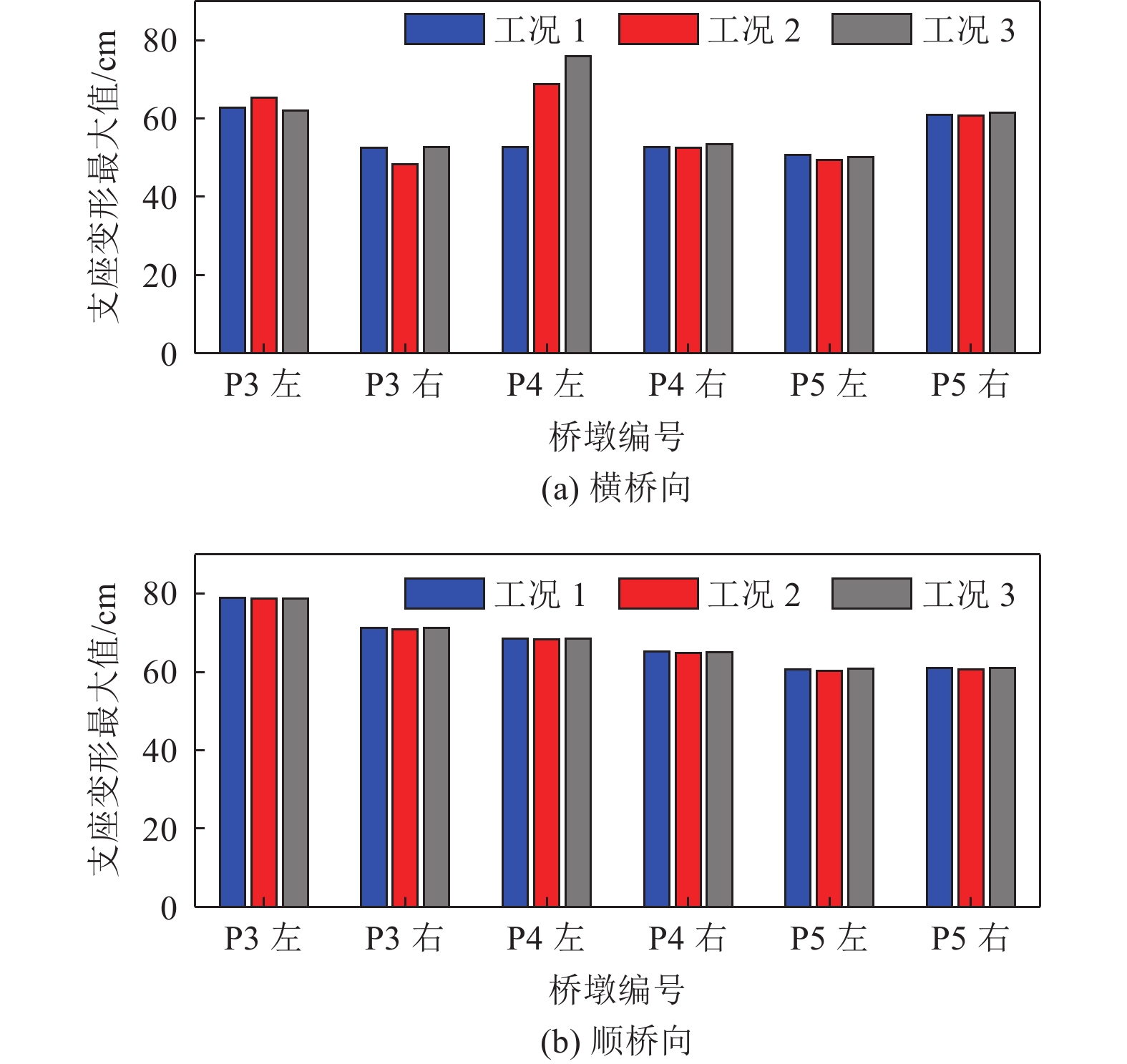
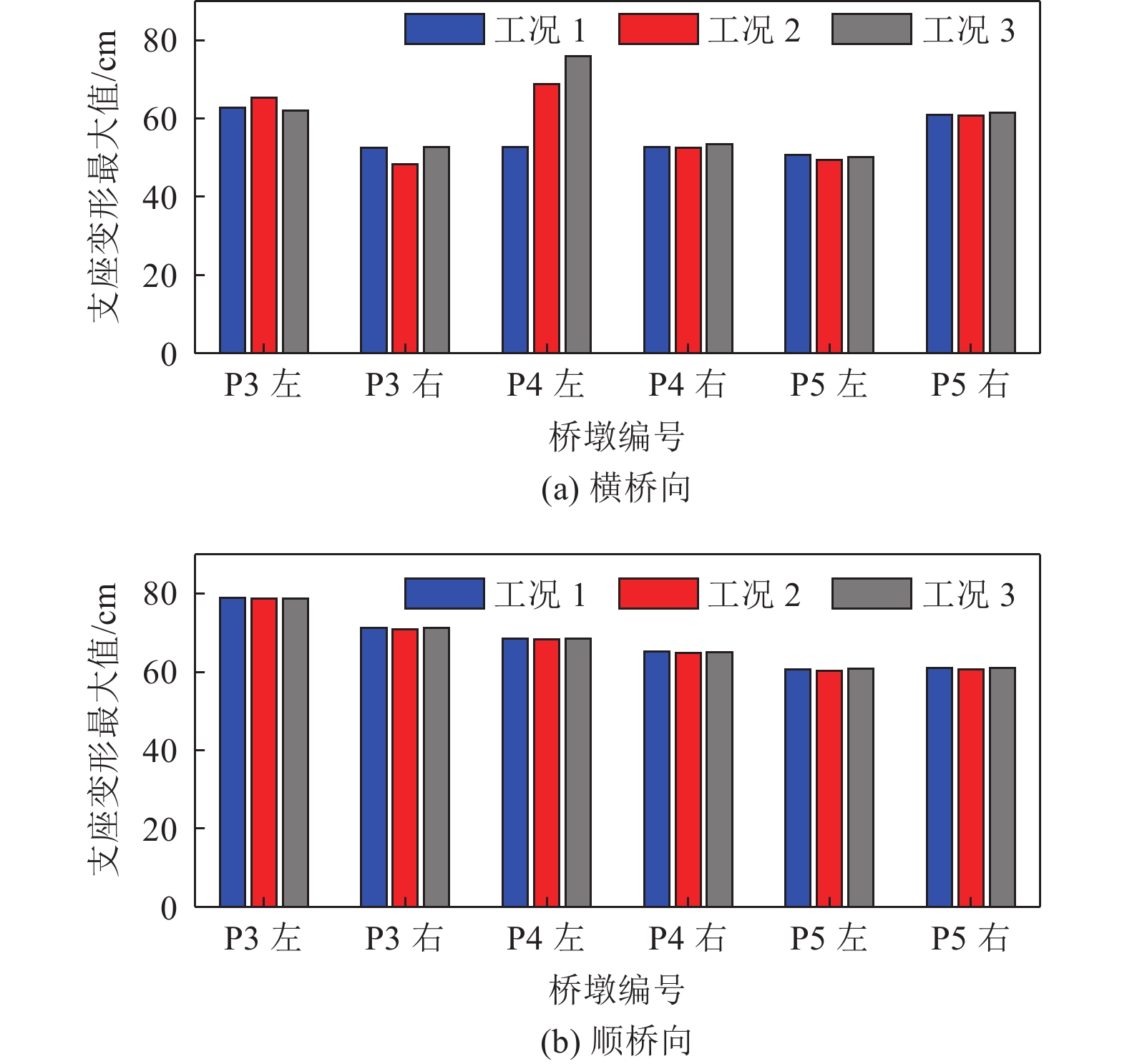
3种工况下横桥向和顺桥向的桥墩支座变形最大值如图7。从计算结果可以看出，非一致地震动作用模式（工况2）和一致地震动作用模式（工况1）的地震动输入导致桥墩支座横桥向变形反应计算结果在断层两侧最靠近断层的桥墩处产生较大差异。这说明地震动永久性位移会使桥梁的计算桥墩支座变形发生显著变化；同时，非一致地震动作用模式（工况2）与一致地震动作用叠加断层错动位移静力作用（工况3）结果的比较，表明两者有较好的一致性，工况3也能较好地反映断层两侧地震动（包括永久性位移）差异对桥梁反应桥墩支座变形的影响。
图 7 横桥向和顺桥向桥墩支座变形最大值Figure 7. Maximum deformation of bearing in the transverse direction and longitudinal direction3.3 桥墩墩底剪力
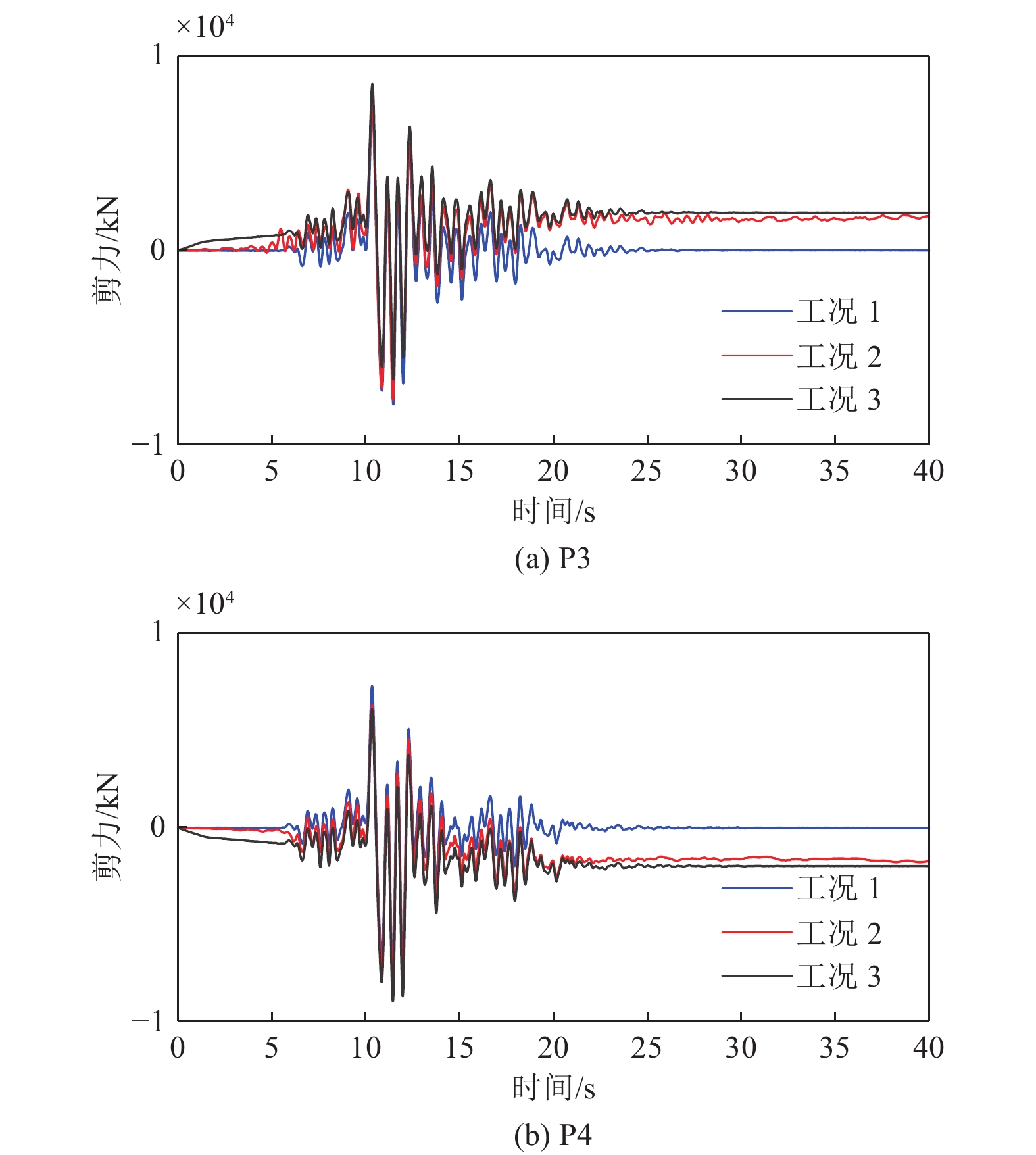
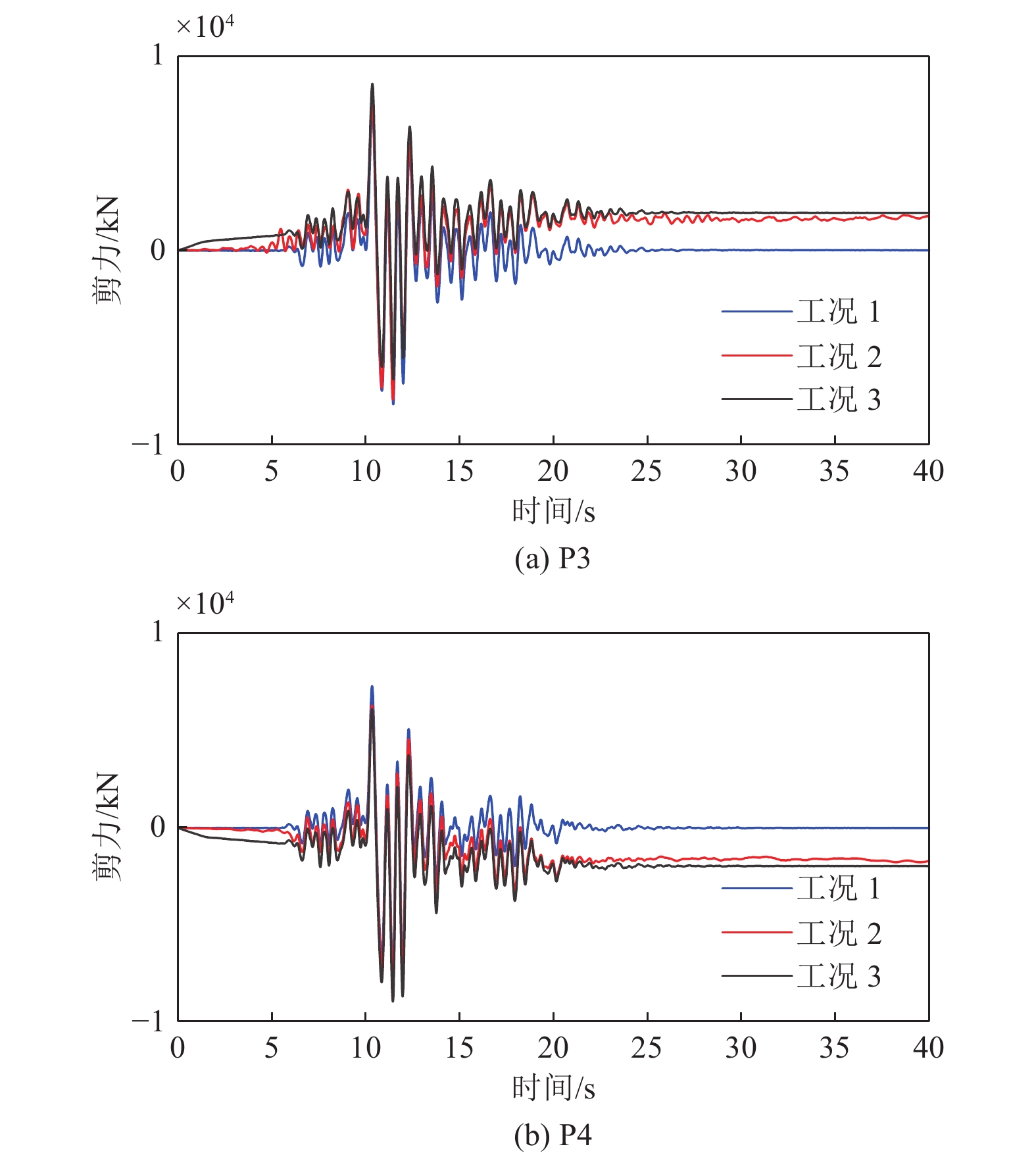
3种工况下横桥向桥墩墩底剪力时程如图8所示，墩底剪力最大值和残余值如表4所示。从计算结果可以看出，墩底剪力时程与墩顶相对位移时程计算结果有类似的差异性趋势，即非一致地震动作用模式（工况2）和一致地震动作用模式（工况1）的地震动输入导致墩底剪力反应计算结果产生较大的差异。这说明地震动永久性位移会使桥梁的计算墩底剪力显著增加；同时，非一致地震动作用模式（工况2）与一致地震动作用叠加断层错动位移静力作用（工况3）结果的比较，表明两者有较好的一致性，工况3也能较好地反映断层两侧地震动（包括永久性位移）差异对桥梁反应墩底剪力的影响。
图 8 横桥向P3和P4墩底剪力时程Figure 8. Shear force time histories at the bottom of the pier P3 and P4 in the transverse direction表 4 横桥向P3和P4墩底剪力最大值和残余值Table 4. The maximum and residual shear force at the bottom of pier P3 and P4 in the transverse direction工况 剪力最大值/kN 残余剪力/kN P3 P4 P3 P4 1 7.9340$ \times {10}^{3} $ 7.6760$ \times {10}^{3} $ 0.0044$ \times {10}^{3} $ −0.0084$ \times {10}^{3} $ 2 7.6930$ \times {10}^{3} $ 8.1211$ \times {10}^{3} $ 1.7479$ \times {10}^{3} $ −1.7280$ \times {10}^{3} $ 3 8.5876$ \times {10}^{3} $ 8.9535$ \times {10}^{3} $ 1.9306$ \times {10}^{3} $ −1.9704$ \times {10}^{3} $ 3.4 桥墩墩底弯矩
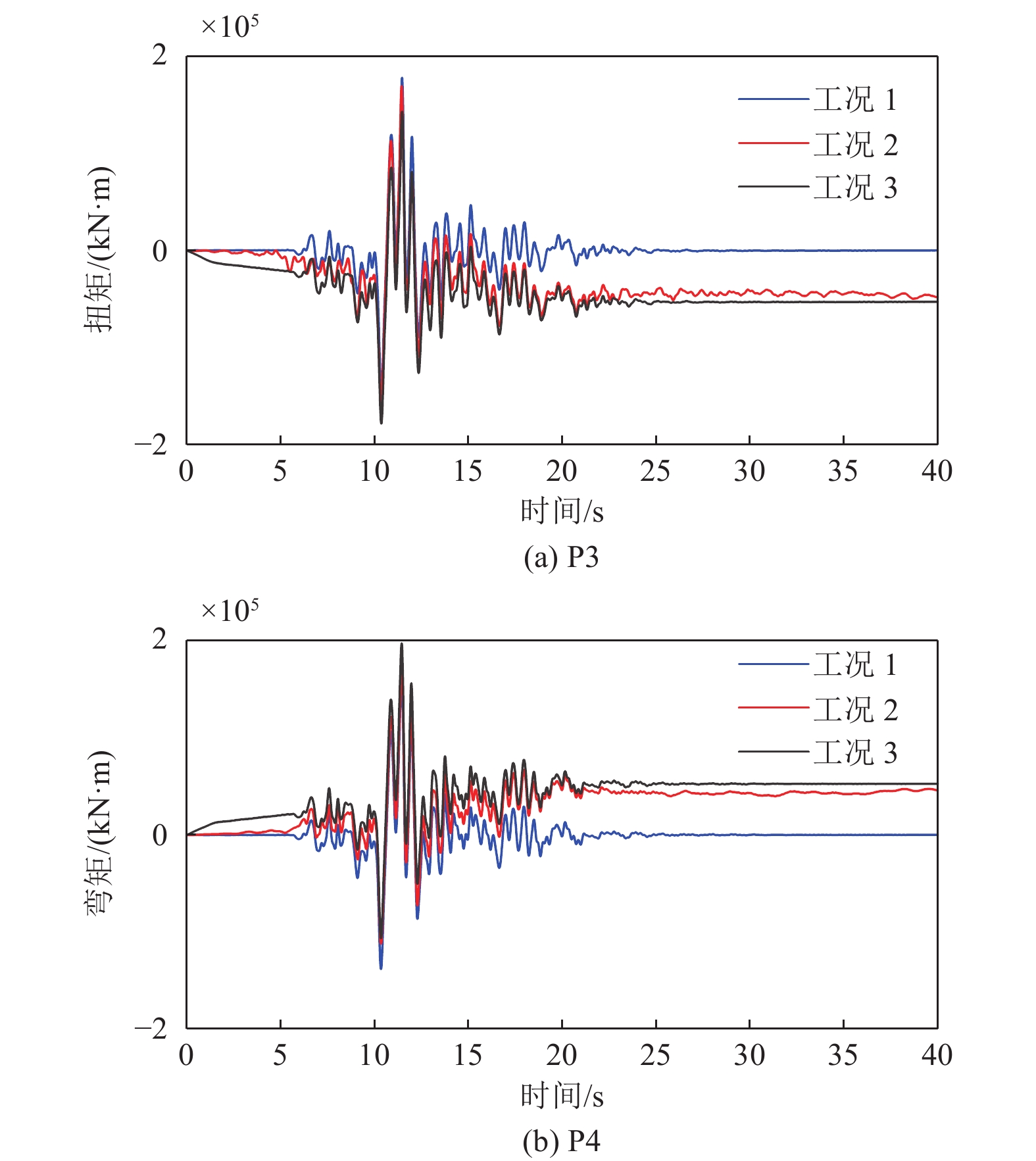
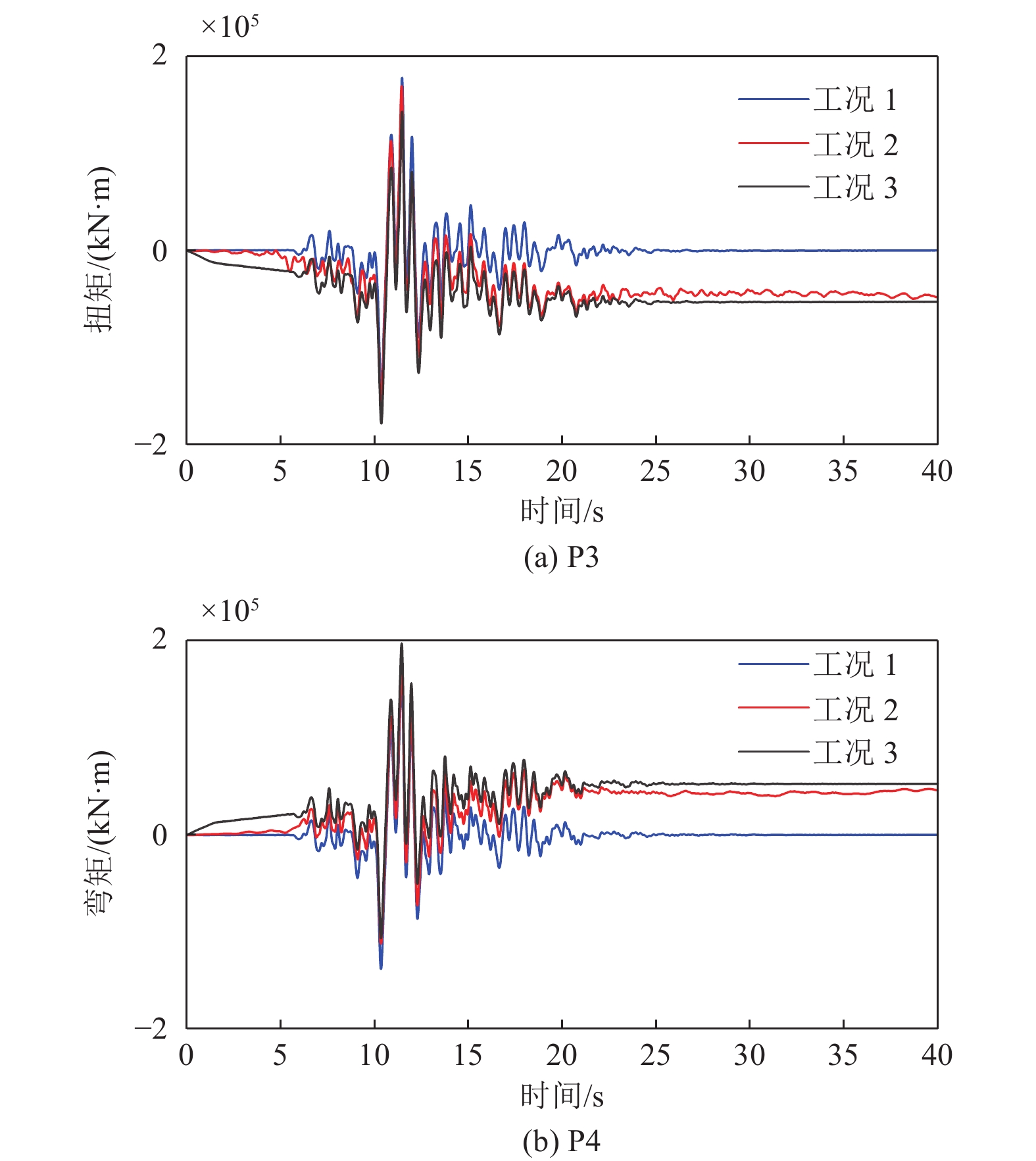
3种工况下横桥向桥墩墩底弯矩时程如图9所示，墩底弯矩最大值和残余值如表5所示。从计算结果可以看出，墩底弯力时程与墩顶相对位移时程和墩底剪力时程计算结果亦有类似的差异性趋势，即非一致地震动作用模式（工况2）和一致地震动作用模式（工况1）的地震动输入导致墩底弯矩反应计算结果产生较大差异。这说明地震动永久性位移会使桥梁的计算墩底弯矩显著增加；同时，非一致地震动作用模式（工况2）与一致地震动作用叠加断层错动位移静力作用（工况3）结果的比较，表明两者有较好的一致性，工况3也能较好地反映断层两侧地震动（包括永久性位移）差异对桥梁反应墩底弯矩的影响，包括断层两侧离断层最近的桥墩P3和P4，其最大值和残余值基本相同。
图 9 横桥向P3和P4墩底弯矩时程Figure 9. Bending moment time histories of at the bottom of the pier P3 and P4 in the transverse direction表 5 横桥向P3和P4墩底弯矩最大值和残余值Table 5. The maximum and residual bending moment at the bottom of pier P3 and P4 in the transverse direction工况 弯矩最大值 /（kN∙m） 残余弯矩 /（kN∙m） P3 P4 P3 P4 1 1.7790$ \times {10}^{5} $ 1.6317$ \times {10}^{5} $ 0.0016$ \times {10}^{4} $ 0.0328$ \times {10}^{4} $ 2 1.6921$ \times {10}^{5} $ 1.7596$ \times {10}^{5} $ 4.7504$ \times {10}^{4} $ 4.6370$ \times {10}^{4} $ 3 1.7830$ \times {10}^{5} $ 1.9733$ \times {10}^{5} $ 5.2868$ \times {10}^{4} $ 5.2781$ \times {10}^{4} $ 3.5 桥墩墩底扭矩
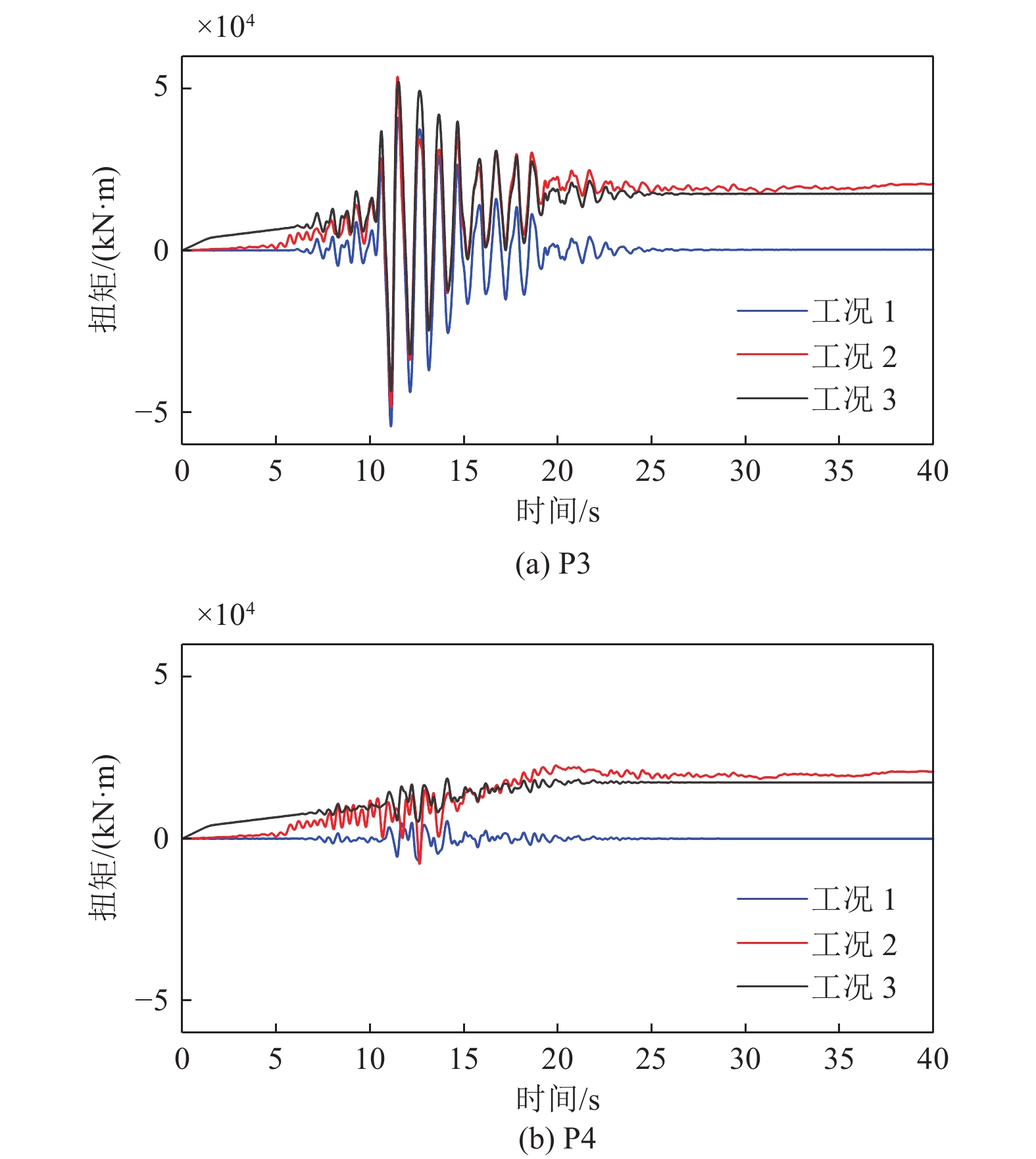
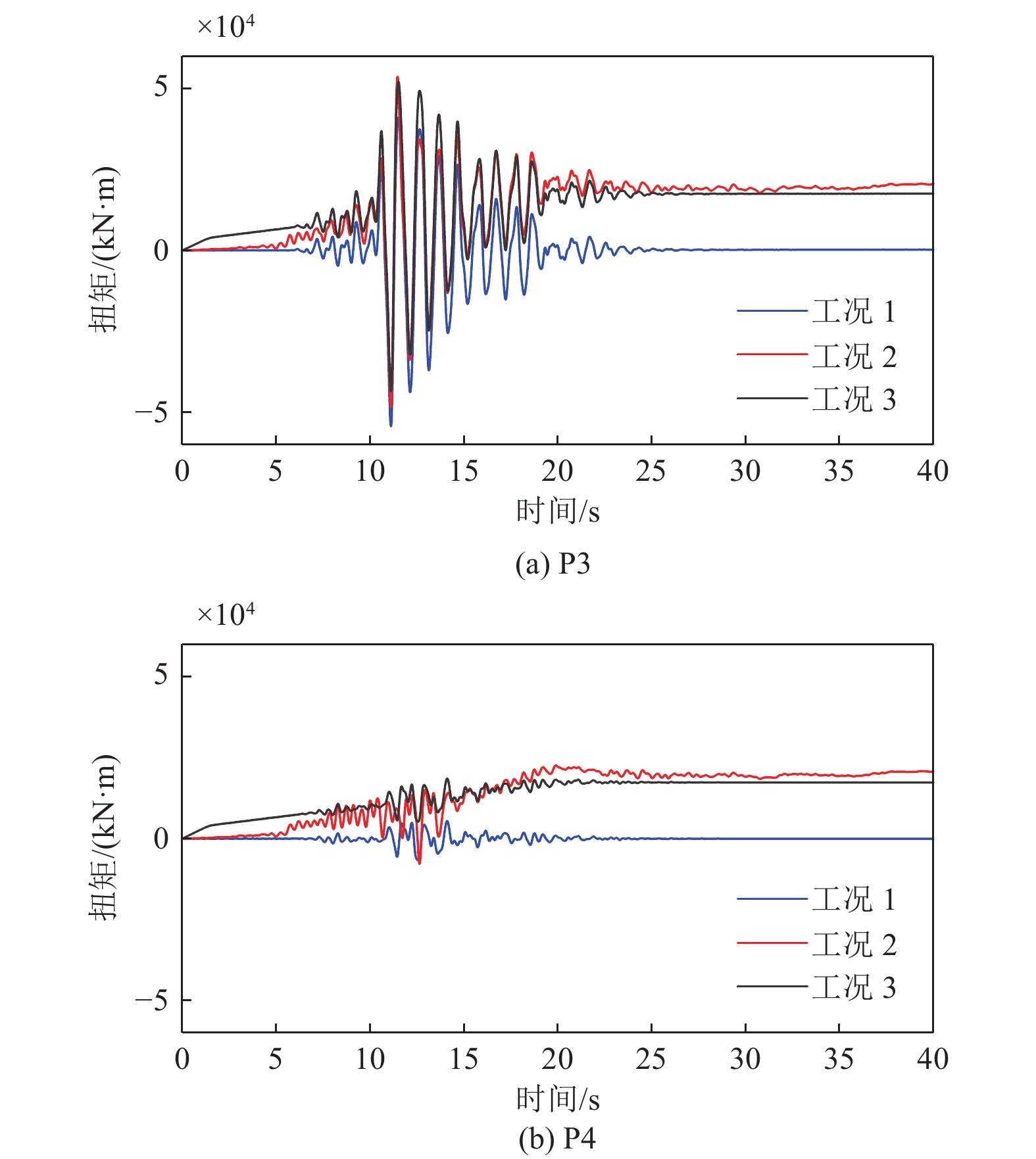
3种工况下横桥向桥墩墩底扭矩时程如图10所示，墩底扭矩最大值和残余值如表6所示。从计算结果可以看出，非一致地震动作用模式（工况2）和一致地震动作用模式（工况1）的地震动输入导致墩底扭矩反应计算结果产生较大的差异。这说明地震动永久性位移会使桥梁的计算墩底扭矩显著增加；非一致地震动作用模式（工况1）与一致地震动作用叠加断层错动位移静力作用（工况3）结果的比较，表明两者之间的差异显著减小，但与其它反应量相比，墩底扭矩计算值之间的差异要明显，这同样也说明工况3能反映断层两侧地震动（包括永久性位移）差异对桥梁反应墩底扭矩的影响，但其计算值还有一定程度的低估，这一点值得进一步关注。
图 10 P3和P4墩底扭矩时程Figure 10. Torque time histories of at the bottom of the pier P3 and P4 in the transverse direction表 6 P3和P4墩底扭矩最大值和残余值Table 6. The maximum and residual torque at the bottom of pier P3 and P4 in the transverse direction工况 扭矩最大值 /（kN∙m） 残余扭矩 /（kN∙m） P3 P4 P3 P4 1 5.4362$ \times {10}^{4} $ 0.6780$ \times {10}^{4} $ 0.0225$ \times {10}^{4} $ 0.0054$ \times {10}^{4} $ 2 5.3635$ \times {10}^{4} $ 2.2612$ \times {10}^{4} $ 2.0436$ \times {10}^{4} $ 2.0624$ \times {10}^{4} $ 3 5.2122$ \times {10}^{4} $ 1.8589$ \times {10}^{4} $ 1.7523$ \times {10}^{4} $ 1.7337$ \times {10}^{4} $ 综上所述，非一致地震动作用模式和一致地震动作用模式的地震动输入会导致桥梁反应计算结果产生很大差异。这说明断层两侧地震动永久性位移差异的考虑会使桥梁反应的计算结果显著增加，这是一致地震动作用模式的地震动输入所不能考虑的。而一致地震动作用叠加断层错动位移静力作用的组合地震作用模式的结果与非一致地震动作用模式结果的比较，桥梁结构反应量计算结果之间的差异较小。计算分析结果进一步说明，在一定近似程度上讲，采用一致地震动作用叠加永久位移静力作用的等效组合模式可以有效地模拟实际地震作用状况下跨断层桥梁结构地震反应，这样也可以避开考虑永久位移地震动作用的结构反应模拟的复杂问题。
4. 结语
针对跨断层桥梁工程结构，计算分析了断层发震引起的断层两侧具有永久位移差异的地震动作用下结构地震反应特征，重点探讨了不同地震作用输入模式对桥梁结构地震反应计算结果的影响。研究得到了以下结论：
（1）计算分析3种地震作用模式（有永久位移非一致地震动作用模式、无永久位移一致地震动作用模式、断层错动位移静力作用模式）的桥梁基础地震动输入下结构地震反应，展现了断层两侧地震动永久位移差异对桥梁结构反应的计算结果有显著影响，永久位移差异会较大程度地加大桥梁结构地震反应。
（2）如果在一致地震动作用桥梁结构地震反应的基础上，叠加断层错动位移静力作用的结构反应，计算得到的结构反应与具有永久位移差异的非一致地震动作用的桥梁结构地震反应十分接近，特别是反应的最大值和残余值。
（3）在一定近似程度上讲，跨断层桥梁结构地震反应可采用一致地震动作用叠加永久位移静力作用的等效地震作用方法模拟。
本文基于算例计算分析，探讨了跨越发震断层桥梁结构地震反应及地震作用输入的有效处理方法，可为相关问题解决提供研究思路与参考。由于算例的特定性，本文仅考虑了桥梁正交跨越走滑断层这一特殊情况，所展现的研究结果有其局限性和普适性问题，有待于更多算例研究加以确认或订正。
-
图 3 场地基岩水平向地震加速度反应谱
Figure 3. Horizontal seismic acceleration response spectrum of rock site
图 4 不考虑永久位移的人工合成地震动时程
Figure 4. Synthetic ground motion time histories without considering permanent displacement
图 5 横桥向考虑永久位移的人工合成地震动时程
Figure 5. Synthetic ground motion time history considering permanent displacement in the transverse direction
图 6 横桥向P3和P4墩顶相对位移时程
Figure 6. Relative displacement time histories on the top of pier P3 and P4 in the transverse direction
图 7 横桥向和顺桥向桥墩支座变形最大值
Figure 7. Maximum deformation of bearing in the transverse direction and longitudinal direction
图 8 横桥向P3和P4墩底剪力时程
Figure 8. Shear force time histories at the bottom of the pier P3 and P4 in the transverse direction
图 9 横桥向P3和P4墩底弯矩时程
Figure 9. Bending moment time histories of at the bottom of the pier P3 and P4 in the transverse direction
图 10 P3和P4墩底扭矩时程
Figure 10. Torque time histories of at the bottom of the pier P3 and P4 in the transverse direction
表 1 原始地震动时程信息
Table 1. Original ground motion parameters
方向 PGA /g PGV/（cm·s−1） PGD/cm 横桥向 0.73 133.33 113.87 顺桥向 0.79 28.09 25.52 
下载: 导出CSV
表 2 合成的地震动时程信息
Table 2. Synthetic ground motion parameters
类别 PGA /g PGV /（cm·s−1） PGD /cm 横桥向不考虑永久位移 0.60 111.97 105.39 横桥向考虑永久位移 0.60 117.79 138.88 顺桥向不考虑永久位移 0.60 118.89 110.84
下载: 导出CSV
表 3 横桥向P3和P4墩顶相对位移最大值和残余值
Table 3. Maximum and residual relative displacement of the pier top at P3 and P4 in the transverse direction
工况 最大值/cm
（残余值/cm）P2 P3 P4 P5 P6 1 9.0580
（−0.1654）4.6155
（−0.0405）3.8598
（−0.0254）6.4269
（−0.1254）5.5834
（−0.1095）2 9.8470
（0.2830）4.4210
（−1.2270）4.1927
（1.1377）6.3951
（−0.0789）5.5772
（−0.0757）3 9.2286
（0.1558）4.7349
（−1.4285）4.7175
（1.2923）6.4440
（−0.1007）5.5611
（−0.1431）
下载: 导出CSV
表 4 横桥向P3和P4墩底剪力最大值和残余值
Table 4. The maximum and residual shear force at the bottom of pier P3 and P4 in the transverse direction
工况 剪力最大值/kN 残余剪力/kN P3 P4 P3 P4 1 7.9340$ \times {10}^{3} $ 7.6760$ \times {10}^{3} $ 0.0044$ \times {10}^{3} $ −0.0084$ \times {10}^{3} $ 2 7.6930$ \times {10}^{3} $ 8.1211$ \times {10}^{3} $ 1.7479$ \times {10}^{3} $ −1.7280$ \times {10}^{3} $ 3 8.5876$ \times {10}^{3} $ 8.9535$ \times {10}^{3} $ 1.9306$ \times {10}^{3} $ −1.9704$ \times {10}^{3} $
下载: 导出CSV
表 5 横桥向P3和P4墩底弯矩最大值和残余值
Table 5. The maximum and residual bending moment at the bottom of pier P3 and P4 in the transverse direction
工况 弯矩最大值 /（kN∙m） 残余弯矩 /（kN∙m） P3 P4 P3 P4 1 1.7790$ \times {10}^{5} $ 1.6317$ \times {10}^{5} $ 0.0016$ \times {10}^{4} $ 0.0328$ \times {10}^{4} $ 2 1.6921$ \times {10}^{5} $ 1.7596$ \times {10}^{5} $ 4.7504$ \times {10}^{4} $ 4.6370$ \times {10}^{4} $ 3 1.7830$ \times {10}^{5} $ 1.9733$ \times {10}^{5} $ 5.2868$ \times {10}^{4} $ 5.2781$ \times {10}^{4} $
下载: 导出CSV
表 6 P3和P4墩底扭矩最大值和残余值
Table 6. The maximum and residual torque at the bottom of pier P3 and P4 in the transverse direction
工况 扭矩最大值 /（kN∙m） 残余扭矩 /（kN∙m） P3 P4 P3 P4 1 5.4362$ \times {10}^{4} $ 0.6780$ \times {10}^{4} $ 0.0225$ \times {10}^{4} $ 0.0054$ \times {10}^{4} $ 2 5.3635$ \times {10}^{4} $ 2.2612$ \times {10}^{4} $ 2.0436$ \times {10}^{4} $ 2.0624$ \times {10}^{4} $ 3 5.2122$ \times {10}^{4} $ 1.8589$ \times {10}^{4} $ 1.7523$ \times {10}^{4} $ 1.7337$ \times {10}^{4} $
下载: 导出CSV
-
陈令坤, 张楠, 夏禾, 2016. 方向脉冲及竖向效应对高铁桥梁地震响应影响. 振动工程学报, 29（4）: 704—713Chen L. K. , Zhang N. , Xia H. , 2016. Effects of directivity pulse and vertical earthquake on seismic response of high-speed railway bridge. Journal of Vibration Engineering, 29(4): 704—713. (in Chinese) 杜修力, 韩强, 李忠献等, 2008.5. 12汶川地震中山区公路桥梁震害及启示. 北京工业大学学报, 34（12）: 1270—1279Du X. L. , Han Q. , Li Z. X. , et al. , 2008. The seismic damage of bridges in the 2008 Wenchuan earthquake and lessons from its damage. Journal of Beijing University of Technology, 34(12): 1270—1279. (in Chinese) 管仲国, 游瀚, 郭河, 2016. 近断层斜拉桥弹塑性索与阻尼器组合横向减震. 同济大学学报（自然科学版）, 44（11）: 1653—1659Guan Z. G. , You H. , Guo H. , 2016. Responses of cable-stayed bridge transversely isolated with elasto-plastic cable pairs and fluid viscous damper subjected to near fault ground motions. Journal of Tongji University (Natural Science), 44(11): 1653—1659. (in Chinese) 惠迎新, 王克海, 李冲, 2014. 跨断层地表破裂带桥梁震害研究及抗震概念设计. 公路交通科技, 31（10）: 51—57 doi: 10.3969/j.issn.1002-0268.2014.10.009Hui Y. X. , Wang K. H. , Li C. , 2014. Study of seismic damage and seismic conceptual design of bridges across fault surface rupture zones. Journal of Highway and Transportation Research and Development, 31(10): 51—57. (in Chinese) doi: 10.3969/j.issn.1002-0268.2014.10.009 惠迎新, 王克海, 2015 a. 基于多点激励位移输入模型的跨断层桥梁地震动输入方法. 东南大学学报（自然科学版）, 45（3）: 557—562Hui Y. X. , Wang K. H. , 2015 a. Earthquake motion input method for bridges crossing fault based on multi-support excitation displacement input model. Journal of Southeast University (Natural Science Edition), 45(3): 557—562. (in Chinese) 惠迎新, 王克海, 2015 b. 跨断层桥梁地震响应特性研究. 桥梁建设, 45（3）: 70—75Hui Y. X. , Wang K. H. , 2015 b. Study of seismic response features of bridges crossing faults. Bridge Construction, 45(3): 70—75. (in Chinese) 惠迎新, 王克海, 吴刚等, 2015 c. 跨断层桥梁地震响应分析及合理跨越角度研究. 振动与冲击, 34（13）: 6—11, 17Hui Y. X. , Wang K. H. , Wu G. , et al. , 2015 c. Seismic responses of bridges crossing faults and their best crossing angles. Journal of Vibration and Shock, 34(13): 6—11, 17. (in Chinese) 惠迎新, 台玉吉, 王克海等, 2017. 跨断层桥梁抗震若干问题探讨. 地震工程学报, 39（5）: 870—875, 889Hui Y. X. , Tai Y. J. , Wang K. H. , et al. , 2017. Discussion about earthquake resistance of the bridges crossing the active fault. China Earthquake Engineering Journal, 39(5): 870—875, 889. (in Chinese) 江辉, 朱晞, 倪永军, 2011. 基于谱分析与RC梁桥检验的脉冲型近场地震动强度度量指标. 铁道学报, 33（3）: 91—99 doi: 10.3969/j.issn.1001-8360.2011.03.016Jiang H. , Zhu X. , Ni Y. J. , 2011. Intensity indice of impulsive near-fault earthquake ground motion based on spectra analysis and RC bridge check. Journal of the China Railway Society, 33(3): 91—99. (in Chinese) doi: 10.3969/j.issn.1001-8360.2011.03.016 李鸿晶, 陆鸣, 温增平等, 2009. 汶川地震桥梁震害的特征. 南京工业大学学报（自然科学版）, 31（1）: 24—29Li H. J. , Lu M. , Wen Z. P. , et al. , 2009. Characteristics of bridge damages in Wenchuan earthquake. Journal of Nanjing University of Technology (Natural Science Edition), 31(1): 24—29. (in Chinese) 李建中, 管仲国, 2011. 基于性能桥梁抗震设计理论发展. 工程力学, 28（S2）: 24—30, 53Li J. Z. , Guan Z. G. , 2011. Performance-based seismic design for bridges. Engineering Mechanics, 28(S2): 24—30, 53. (in Chinese) 李帅, 张凡, 颜晓伟等, 2017. 近断层地震动合成方法及其对超大跨斜拉桥地震响应影响. 中国公路学报, 30（2）: 86—97, 106Li S. , Zhang F. , Yan X. W. , et al. , 2017. Synthetic method for near-fault ground motions and its influence on seismic response of super-span cable-stayed bridge. China Journal of Highway and Transport, 30(2): 86—97, 106. (in Chinese) 李小军, 1992. 场地土层对地震地面运动影响的分析方法. 世界地震工程, 8（2）: 49—60. 李小军, 彭青, 2001. 不同类别场地地震动参数的计算分析. 地震工程与工程振动, 21（1）: 29—36Li X. J. , Peng Q. , 2001. Calculation and analysis of earthquake ground motion parameters for different site categories. Earthquake Engineering and Engineering Vibration, 21(1): 29—36. (in Chinese) 李小军, 贺秋梅, 亓兴军, 2012. 地震动速度脉冲对大跨斜拉桥减震控制的影响. 应用基础与工程科学学报, 20（2）: 272—285Li X. J. , He Q. M. , Qi X. J. , 2012. Seismic mitigation control effects of long-span cable-stayed bridges to ground motions with velocity pulse. Journal of Basic Science and Engineering, 20(2): 272—285. (in Chinese) 刘爱文, 夏珊, 徐超, 2008. 汶川地震交通系统震害及震后抢修. 震灾防御技术, 3（3）: 243—450.Liu A. W., Xia S., Xu C., 2008. Damage and emergency recovery of the transportation systems after Wenchuan earthquake. Technology for Earthquake Disaster Prevention, 3（3）: 243–250. (in Chinese) 刘启方, 袁一凡, 金星等, 2006. 近断层地震动的基本特征. 地震工程与工程振动, 26（1）: 1—10Liu Q. F. , Yuan Y. F. , Jin X. , et al. , 2006. Basic characteristics of near-fault ground motion. Earthquake Engineering and Engineering Vibration, 26(1): 1–10. (in Chinese) 石岩, 王东升, 孙治国, 2014. 近断层地震动下减隔震桥梁地震反应分析. 桥梁建设, 44（3）: 19—24Shi Y. , Wang D. S. , Sun Z. G. , 2014. Analysis of seismic response of seismically mitigated and isolated bridge subjected to near-fault ground motion. Bridge Construction, 44(3): 19—24. (in Chinese) 王东升, 杨海红, 王国新, 2005. 考虑邻梁碰撞的多跨长简支梁桥落梁震害分析. 中国公路学报, 18（3）: 54—59Wang D. S. , Yang H. H. , Wang G. X. , 2005. Seismic analysis of girders falling down in multi-span long simply supported bridges with adjacent pounding effects. China Journal of Highway and Transport, 18(3): 54—59. (in Chinese) 王东升, 郭迅, 孙治国等, 2009. 汶川大地震公路桥梁震害初步调查. 地震工程与工程振动, 29（3）: 84—94Wang D. S. , Guo X. , Sun Z. G. , et al. , 2009. Damage to highway bridges during Wenchuan earthquake. Journal of Earthquake Engineering and Engineering Vibration, 29(3): 84—94. (in Chinese) 王东升, 孙治国, 李晓莉等, 2010. 汶川大地震曲线梁桥震害及破坏机理分析. 防灾减灾工程学报, 30（5）: 572—579Wang D. S. , Sun Z. G. , Li X. L. , et al. , 2010. Seismic damage investigation and failure mechanism analysis of curved bridges in Wenchuan earthquake. Journal of Disaster Prevention and Mitigation Engineering, 30(5): 572—579. ( in Chinese 杨怀宇, 李建中, 2015. 断层地震动对隔震桥梁地震响应的影响. 同济大学学报（自然科学版）, 43（8）: 1144—1152Yang H. Y. , Li J. Z. , 2015. Response analysis of seismic isolated bridge under influence of fault-crossing groundmotions. Journal of Tongji University (Natural Science), 43(8): 1144—1152. (in Chinese) 袁一凡, 田启文, 2012. 工程地震学. 北京: 地震出版社. 中华人民共和国交通运输部, 2014. JTG B02—2013 公路工程抗震规范. 北京: 人民交通出版社.Ministry of Transport of the People's Republic of China, 2014. JTG B02—2013 Specification of seismic design for highway engineering. Beijing: China Communications Press. (in Chinese) 中华人民共和国交通运输部, 2020. JTG/T 2231-01—2020 公路桥梁抗震设计规范. 北京: 人民交通出版社.Ministry of Transport of the People's Republic of China, 2020. JTG/T2231-01—2020 Specifications for seismic design of highway bridges. Beijing: China Communications Press. (in Chinese) 中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2010. GB 50011—2010 建筑抗震设计规范. 北京: 中国建筑工业出版社.Ministry of Housing and Urban-Rural Development of the People’s Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, 2010. GB 50011—2010 Code for seismic design of buildings. Beijing: China Architecture & Building Press. (in Chinese) 周正华, 张艳梅, 孙平善等, 2003. 断层场地震害研究综述. 地震工程与工程振动, 23（5）: 38—41 doi: 10.3969/j.issn.1000-1301.2003.05.006Zhou Z. H. , Zhang Y. M. , Sun P. S. , et al. , 2003. A summary of damage study on fault site. Earthquake Engineering and Engineering Vibration, 23(5): 38—41. (in Chinese) doi: 10.3969/j.issn.1000-1301.2003.05.006 Byers W. G. , Edwards C. , Tang A. , et al. , 2000. Performance of transportation systems after the 1999 Kocaeli earthquake. Earthquake Spectra, 16(S1): 403—410. Caltrans, 2012. Bridge design practice . Sacramento: California Department of Transportation. Caltrans, 2019. Seismic design criteria: version 2.0. Sacramento: California Department of Transportation. CEN, 2004. EN 1998-5—2004 Eurocode 8: design of structures for earthquake resistance Part 5: foundation, retaining structures and geotechnical aspects. Brussels: European Committee for Standardization, 14—20. Chang K. C. , Chang D. W. , Tsai M. H. , et al. , 2000. Seismic performance of highway bridges. Earthquake Engineering and Engineering Seismology, 2(1): 55—77. Elgamal A., Lu J., Mackie K., 2014. MSBrindge: OpenSees pushover and earthquake analysis of multi-span bridges - User Manual. San Diego: Department of Structural Engineering, University of California. Ghasemi H., Cooper J. D., Imbsen R., et al., 2000. The November 1999 Duzce earthquake: post-earthquake investigation of the structures on the TEM. Washington: Federal Highway Administration. Goel R. , Qu B. , Tures J. , et al. , 2014. Validation of fault rupture-response spectrum analysis method for curved bridges crossing strike-slip fault rupture zones. Journal of Bridge Engineering, 19(5): 06014002. doi: 10.1061/(ASCE)BE.1943-5592.0000602 Goel R. K., Chopra A. K., 2008. Analysis of ordinary bridges crossing fault-rupture zones. In: The 14 th World Conference on Earthquake Engineering. Beijing. Goel R. K. , Chopra A. K. , 2009 a. Linear analysis of ordinary bridges crossing fault-rupture zones. Journal of Bridge Engineering, 14(3): 203—215. doi: 10.1061/(ASCE)1084-0702(2009)14:3(203) Goel R. K. , Chopra A. K. , 2009 b. Nonlinear analysis of ordinary bridges crossing fault-rupture zones. Journal of Bridge Engineering, 14(3): 216—224. doi: 10.1061/(ASCE)1084-0702(2009)14:3(216) Güney D. , Acar M. , Özlüdemir M. T. , et al. , 2010. Investigation of post-earthquake displacements in viaducts using Geodetic and Finite Element Methods. Natural Hazards and Earth System Sciences, 10(12): 2579—2587. doi: 10.5194/nhess-10-2579-2010 He W. L. , Agrawal A. K. , 2008. Analytical model of ground motion pulses for the design and assessment of seismic protective systems. Journal of Structural Engineering, 134(7): 1177—1188. doi: 10.1061/(ASCE)0733-9445(2008)134:7(1177) Hsu Y. T. , Fu C. C. , 2004. Seismic effect on highway bridges in Chi Chi earthquake. Journal of Performance of Constructed Facilities, 18(1): 47—53. doi: 10.1061/(ASCE)0887-3828(2004)18:1(47) Imbsen R. A. , Roblee C. J. , Yashinsky M. , et al. , 2000. Impact on highway structures. Earthquake Spectra, 16(S1): 411—435. Kitagawa Y. , Hiraishi H. , 2004. Overview of the 1995 Hyogo-Ken Nanbu earthquake and proposals for earthquake mitigation measures. Journal of Japan Association for Earthquake Engineering, 4 (3): 1—29. doi: 10.5610/jaee.4.3_1 Li S. , Zhang F. , Wang J. Q. , et al. , 2017. Effects of near-fault motions and artificial pulse-type ground motions on super-span cable-stayed bridge systems. Journal of Bridge Engineering, 22(3): 04016128. doi: 10.1061/(ASCE)BE.1943-5592.0001008 Mackie K. R. , Lu J. C. , Elgamal A. , 2012. Performance-based earthquake assessment of bridge systems including ground-foundation interaction. Soil Dynamics and Earthquake Engineering, 42: 184—196. doi: 10.1016/j.soildyn.2012.05.023 Makris N. , Chang S. P. , 2000. Effect of viscous, viscoplastic and friction damping on the response of seismic isolated structures. Earthquake Engineering & Structural Dynamics, 29(1): 85—107. Mavroeidis G. P. , Papageorgiou A. S. , 2003. A mathematical representation of near-fault ground motions. Bulletin of the Seismological Society of America, 93(3): 1099—1131. doi: 10.1785/0120020100 Park S. W. , Ghasemi H. , Shen J. , et al. , 2004. Simulation of the seismic performance of the Bolu Viaduct subjected to near‐fault ground motions. Earthquake Engineering & Structural Dynamics, 33(13): 1249—1270. Roussis P. C. , Constantinou M. C. , Erdik M. , et al. , 2003. Assessment of performance of seismic isolation system of bolu viaduct. Journal of Bridge Engineering, 8(4): 182—190. doi: 10.1061/(ASCE)1084-0702(2003)8:4(182) Sehhati R. , Rodriguez-Marek A. , ElGawady M. , et al. , 2011. Effects of near-fault ground motions and equivalent pulses on multi-story structures. Engineering Structures, 33(3): 767—779. doi: 10.1016/j.engstruct.2010.11.032 Sengupta A. , Quadery L. , Sarkar S. , et al. , 2016. Influence of bidirectional near-fault excitations on RC bridge piers. Journal of Bridge Engineering, 21(7): 04016034. doi: 10.1061/(ASCE)BE.1943-5592.0000836 Somerville P. G., 2003. Magnitude scaling of the near fault rupture directivity pulse. Physics of the Earth and Planetary Interiors, 137(1—4): 201—212. Wang N. , Elgamal A. , Shantz T. , 2017. Recorded seismic response of the Samoa Channel Bridge-foundation system and adjacent downhole array. Soil Dynamics and Earthquake Engineering, 92: 358—376. doi: 10.1016/j.soildyn.2016.09.034 Yan G. Y. , Chen F. Q. , 2015. Seismic performance of midstory isolated structures under near-field pulse-like ground motion and limiting deformation of isolation layers. Shock and Vibration, 2015: 730612. Yang S. , Mavroeidis G. P. , 2018. Bridges crossing fault rupture zones: a review. Soil Dynamics and Earthquake Engineering, 113: 545—571. doi: 10.1016/j.soildyn.2018.03.027 期刊类型引用(1)
1. 王燕航，刘浪. 近断层桥梁抗震的人工合成地震动. 工程建设. 2024(07): 40-45 . 
百度学术其他类型引用(1)
-
下载:
点击查看大图
计量
- 文章访问数: 263
- HTML全文浏览量: 113
- PDF下载量: 94
- 被引次数: 2
